20-10-2013, 8:54 PM
Hallar la ecuación de la recta tangente a la cónica en el punto dado:
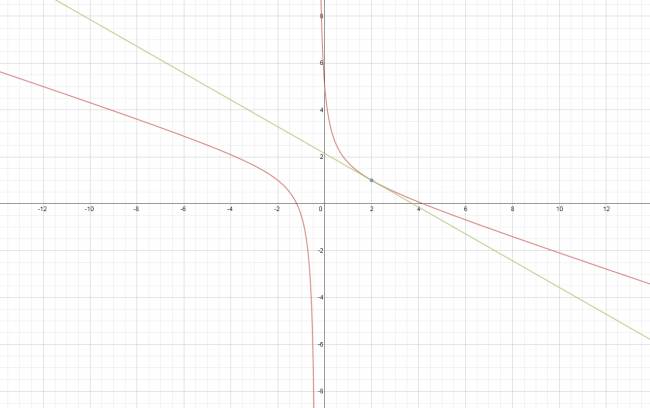
a. \( x^2 + 3·x·y - 3·x + y - 5 = 0 \) en A(2,1)
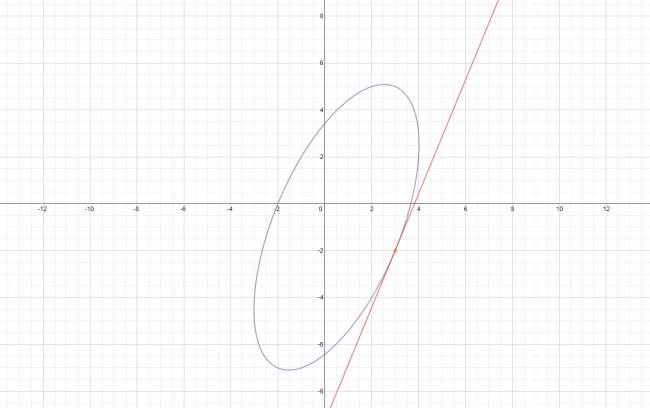
b. \( 3·x^2 - 2·x·y + y^2 - 5·x + 3·y - 22 = 0 \) en P(3,-2)
a. \( x^2 + 3·x·y - 3·x + y - 5 = 0 \) en A(2,1)
b. \( 3·x^2 - 2·x·y + y^2 - 5·x + 3·y - 22 = 0 \) en P(3,-2)