| Foro Problemas resueltos Cálculo del área debajo de la curva en un cierto intervalo |
| Cálculo del área debajo de la curva en un cierto intervalo |
09-11-2013, 5:04 AM
Calcular el área debajo de las siguientes curvas en las siguientes situaciones.
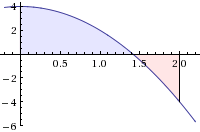
1. \( f(x) = -2·x^2 + 4 \) en el intervalo [0,2] 2. Calcule el siguiente área en el intervalo: [0,3]:  |
09-11-2013, 9:46 PM
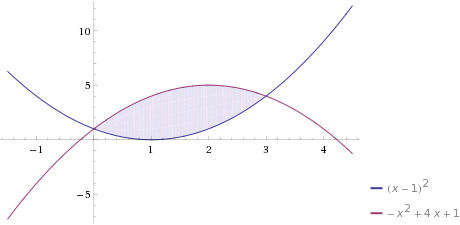
Cita marcos364 (  )1. f(x)=2⋅x2+4 en el intervalo [0,2]  Primero, integraremos la función: \( f(x) = -2·x^2 + 4 ⇒ F(x) = \frac {-2}{3}·x^3 + 4·x \). Ahora aplicamos la regla de Barrow. $$ \int_{0}^{2} -2·x^2 + 4 \, dx = F(2) - F(0) = \frac {8}{3} $$ No se debe aproximar su resultado, pues es bien sabido que es un número racional que tiene infinitos decimales periódicos luego de la coma. Si la aproximáramos, estaríamos escribiendo un valor de un área que no es cierto. Cita Respuesta: El área buscada es: \( á = \frac {8}{3} u^2 \). |
09-11-2013, 9:51 PM
Cita marcos364 ( )2. Calcule el siguiente área en el intervalo: [0,3]: Luego consideraré, otra función \( m/ m(x) = f(x) - g(x) \). Resultando: \( m(x) = 2x^2 - 6·x \). Ahora calcularemos la primitiva de la función hallada. $$ M(x) = \frac {2}{3}·x^3 - 3·x^2 + c, c∈ℝ $$ Aplicamos la regla de Barrow: $$ \int_{0}^{3} 2x^2 - 6·x \, dx = M(3) - M(0) = 9 $$ Cita Respuesta: El área buscada es \( 9 u^2 \). |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.