24-10-2013, 6:43 PM
Elipse
Definición:
Dados dos puntos \( F \) y \( F' \) y un número real positivo \( 2·a \) tal que \( 2·a > d(F,F') \). Se conoce como elipse al lugar geométrico de los puntos del plano cuya suma de distancias a \( F \) y \( F' \) sea igual y constante a \( 2·a \).
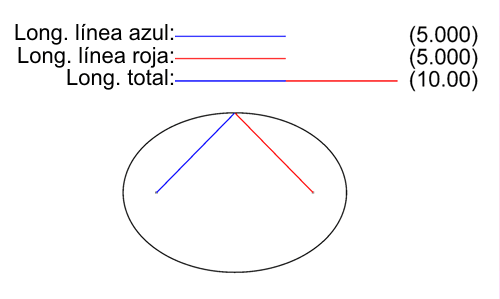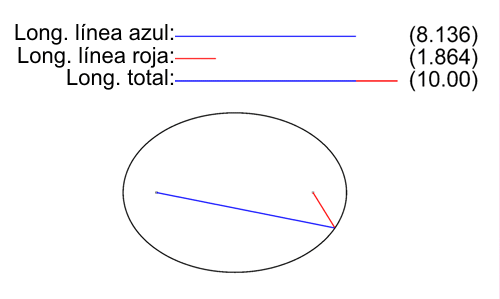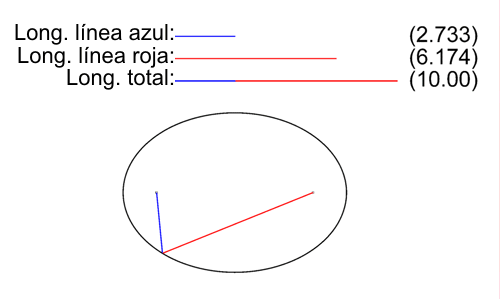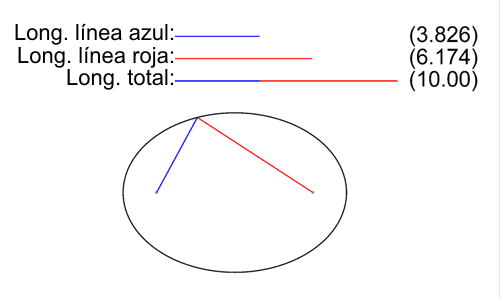
Todo punto P que pertenezca a la elipse debe cumplir que:
$$ ∀P∈ \mathcal{E} ⇔ d(P,F)+d(P,F') = 2·a / 2·a > d(F,F') $$
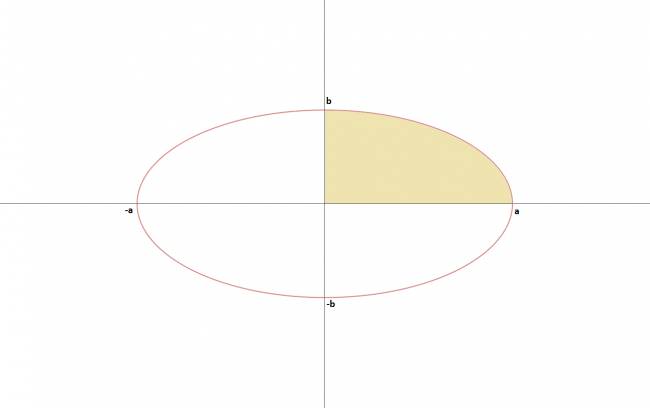
Elementos de una elipse:
· Focos: F y F' \( / d(F,F') = 2·c \)
· Número real positivo \( 2·a∈ℝ^{+} / 2·a > 2·c ⇒ a > c \)
· Ejes de simetría:
:: Eje focal: la recta FF'.
:: Eje transverso: mediatriz de FF'.
· Centro de simetría: O, punto medio de FF'.
· Vértices:
:: A y A' los cuales pertenecen al eje focal.
:: B y B' los cuales pertenecen al eje transverso.
· Longitud del segmento AA': \( d(A,A') = 2·a \)
Ecuación de la elipse:
· Toda elipse de eje focal paralelo a \( O \vec x \) se puede expresar de la forma reducida:
$$ \frac {(x-h)^2}{a^2} + \frac {(y-k)^2}{b^2} = 1 $$
· Toda elipse de eje focal paralelo a \( O \vec y \) se puede expresar de la forma reducida:
$$ \frac {(x-h)^2}{b^2} + \frac {(y-k)^2}{a^2} = 1 $$
Donde su centro es \( O'(h,k) \).
Se debe tener en cuenta que \( a>b \).
La forma desarrollada de una elipse es: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \) que también es la ecuación de cualquier cónica, por
lo cual, no es recomendable trabajar con ella en forma desarrollada.
Definición:
Dados dos puntos \( F \) y \( F' \) y un número real positivo \( 2·a \) tal que \( 2·a > d(F,F') \). Se conoce como elipse al lugar geométrico de los puntos del plano cuya suma de distancias a \( F \) y \( F' \) sea igual y constante a \( 2·a \).

Todo punto P que pertenezca a la elipse debe cumplir que:
$$ ∀P∈ \mathcal{E} ⇔ d(P,F)+d(P,F') = 2·a / 2·a > d(F,F') $$
Elementos de una elipse:
· Focos: F y F' \( / d(F,F') = 2·c \)
· Número real positivo \( 2·a∈ℝ^{+} / 2·a > 2·c ⇒ a > c \)
· Ejes de simetría:
:: Eje focal: la recta FF'.
:: Eje transverso: mediatriz de FF'.
· Centro de simetría: O, punto medio de FF'.
· Vértices:
:: A y A' los cuales pertenecen al eje focal.
:: B y B' los cuales pertenecen al eje transverso.
· Longitud del segmento AA': \( d(A,A') = 2·a \)
Ecuación de la elipse:
· Toda elipse de eje focal paralelo a \( O \vec x \) se puede expresar de la forma reducida:
$$ \frac {(x-h)^2}{a^2} + \frac {(y-k)^2}{b^2} = 1 $$
· Toda elipse de eje focal paralelo a \( O \vec y \) se puede expresar de la forma reducida:
$$ \frac {(x-h)^2}{b^2} + \frac {(y-k)^2}{a^2} = 1 $$
Donde su centro es \( O'(h,k) \).
Se debe tener en cuenta que \( a>b \).
La forma desarrollada de una elipse es: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \) que también es la ecuación de cualquier cónica, por
lo cual, no es recomendable trabajar con ella en forma desarrollada.