16-09-2013, 4:07 AM
Movimiento Circular Uniforme (MCU)
Este tipo de movimiento, es el que se desarrolla, por ejemplo, cuando agarramos una cuerda que tiene atada al final de esta, una pelota.

Otro ejemplo de movimiento circular:

Al ser un movimiento uniforme, diremos que no presenta aceleración o que ésta es nula, de aquí deduciremos que su velocidad será constante. De aquí, podemos sacar en limpio lo siguiente:
$$ \mbox{(MCU) } a = 0 ⇒ v = cte $$
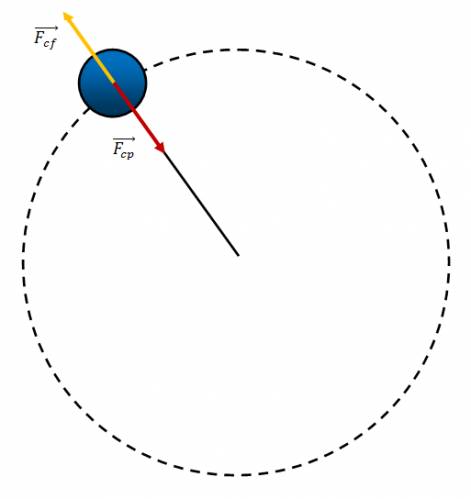
En este tipo de movimiento, existen varias fuerzas, deberemos precisarlas para comprender su estudio. Para todo esto, prestemos atención a la siguiente imagen:
Ahora hablaremos sobre cada una de las fuerzas que intervienen.
· Fuerzas centrípeta \( (\vec F_{cf}) \): es una fuerza constante en magnitud y variable en dirección, dirigida hacia el centro de la circunferencia. Por ejemplo: esta fuerza es la que mantiene al planeta Tierra en órbita, moviéndose al rededor del Sol.
· Fuerza centrífuga \( (\vec F_{cp}) \): es una fuerza ficticia (invento de los físicos, no existe en la realidad, se utiliza para explicar fenómenos, viene a ser la inercia que trata que el cuerpo mantenga una trayectoria rectilínea), tiende a alejar los objetos del centro de rotación del eje mediante la velocidad tangencial, perpendicular al radio, en un movimiento circular. Se puede calcular como:
$$ F_{cp} = m·\frac {v_{t}^2}{R} $$
A todo esto, debemos agregar la velocidad, que siempre es tangente a la trayectoria.
Elementos del movimiento circular:
· Velocidad angular \( ( \omega ) \):
Es el número de vueltas que da el cuerpo, por unidad de tiempo. Se puede calcular como:
$$ \omega = \frac {\Delta \alpha}{\Delta t} \left [ \frac {1}{s} \right ] $$
$$ \omega = \frac {2·\pi}{T} \left [ \frac {1}{s} \right ] $$
$$ \omega = 2·\pi·f \left [ \frac {1}{s} \right ] $$
· Velocidad tangencial \( (v_{t}) \):
Se puede calcular como:
$$ v_{t} = \omega·R \left [ \frac {m}{s} \right ] $$
· Periodo \( (T) \):
Es el tiempo que demora el cuerpo en dar una vuelta completa. Se puede calcular como:
$$ T = \frac {1}{f} \left [ s \right ] $$
· Frecuencia \( (f) \):
Es el número de vueltas que da el cuerpo, por segundo. Se puede calcular como:
$$ f = \frac {1}{T} \left [ Hz \right ] $$
· Aceleración centrípeta \( (a_{c}) \):
Es el causante del cambio de dirección de la velocidad tangencial, siendo perpendicular a esta. Se puede calcular como:
$$ a_{c} = \omega^2·R $$
$$ a_{c} = \frac {v_{t}^2}{R} $$
· Radio \( ( R ) \):
Es el radio de la circunferencia descripta por la trayectoria del cuerpo durante un movimiento circular. Dependiendo de los datos que se conozcan, se puede calcular a través de las fórmulas anteriormente expuestas.
Este tipo de movimiento, es el que se desarrolla, por ejemplo, cuando agarramos una cuerda que tiene atada al final de esta, una pelota.

Otro ejemplo de movimiento circular:

Al ser un movimiento uniforme, diremos que no presenta aceleración o que ésta es nula, de aquí deduciremos que su velocidad será constante. De aquí, podemos sacar en limpio lo siguiente:
$$ \mbox{(MCU) } a = 0 ⇒ v = cte $$
En este tipo de movimiento, existen varias fuerzas, deberemos precisarlas para comprender su estudio. Para todo esto, prestemos atención a la siguiente imagen:
Ahora hablaremos sobre cada una de las fuerzas que intervienen.
· Fuerzas centrípeta \( (\vec F_{cf}) \): es una fuerza constante en magnitud y variable en dirección, dirigida hacia el centro de la circunferencia. Por ejemplo: esta fuerza es la que mantiene al planeta Tierra en órbita, moviéndose al rededor del Sol.
· Fuerza centrífuga \( (\vec F_{cp}) \): es una fuerza ficticia (invento de los físicos, no existe en la realidad, se utiliza para explicar fenómenos, viene a ser la inercia que trata que el cuerpo mantenga una trayectoria rectilínea), tiende a alejar los objetos del centro de rotación del eje mediante la velocidad tangencial, perpendicular al radio, en un movimiento circular. Se puede calcular como:
$$ F_{cp} = m·\frac {v_{t}^2}{R} $$
A todo esto, debemos agregar la velocidad, que siempre es tangente a la trayectoria.
Elementos del movimiento circular:
· Velocidad angular \( ( \omega ) \):
Es el número de vueltas que da el cuerpo, por unidad de tiempo. Se puede calcular como:
$$ \omega = \frac {\Delta \alpha}{\Delta t} \left [ \frac {1}{s} \right ] $$
$$ \omega = \frac {2·\pi}{T} \left [ \frac {1}{s} \right ] $$
$$ \omega = 2·\pi·f \left [ \frac {1}{s} \right ] $$
· Velocidad tangencial \( (v_{t}) \):
Se puede calcular como:
$$ v_{t} = \omega·R \left [ \frac {m}{s} \right ] $$
· Periodo \( (T) \):
Es el tiempo que demora el cuerpo en dar una vuelta completa. Se puede calcular como:
$$ T = \frac {1}{f} \left [ s \right ] $$
· Frecuencia \( (f) \):
Es el número de vueltas que da el cuerpo, por segundo. Se puede calcular como:
$$ f = \frac {1}{T} \left [ Hz \right ] $$
· Aceleración centrípeta \( (a_{c}) \):
Es el causante del cambio de dirección de la velocidad tangencial, siendo perpendicular a esta. Se puede calcular como:
$$ a_{c} = \omega^2·R $$
$$ a_{c} = \frac {v_{t}^2}{R} $$
· Radio \( ( R ) \):
Es el radio de la circunferencia descripta por la trayectoria del cuerpo durante un movimiento circular. Dependiendo de los datos que se conozcan, se puede calcular a través de las fórmulas anteriormente expuestas.