06-09-2013, 10:31 PM
Teorema de Bolzano
Este teorema matemático afirma que si una función \( f(x) \) es continua en un intervalo \( [a,b] \) y se cumple la condición de que \( f(a) \) y \( f(b) \) son de distinto signo, entonces, podemos afirmar que existe al menos una raíz dentro de dicho intervalo.
Esto es algo bastante obvio. Supongamos el siguiente ejemplo:
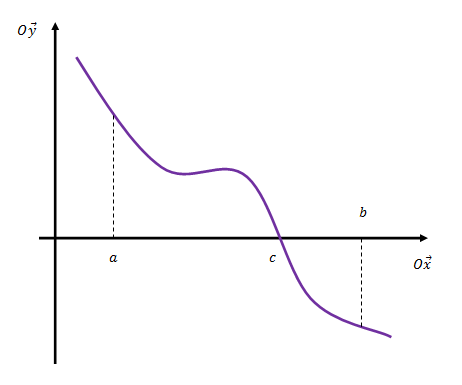
O sea, si una función que es continua, para un valor de abscisa dado tiene una ordenada positiva y para otro valor de abscisa tiene una ordenada negativa, necesariamente, tiene que haber un valor de abscisa que le corresponda una ordenada nula. Dicho en otras palabras, para que la función tenga un parte por arriba del eje horizontal y otra debajo de este, es porque en algún momento se corta con dicho eje.

Este teorema matemático afirma que si una función \( f(x) \) es continua en un intervalo \( [a,b] \) y se cumple la condición de que \( f(a) \) y \( f(b) \) son de distinto signo, entonces, podemos afirmar que existe al menos una raíz dentro de dicho intervalo.
Esto es algo bastante obvio. Supongamos el siguiente ejemplo:

O sea, si una función que es continua, para un valor de abscisa dado tiene una ordenada positiva y para otro valor de abscisa tiene una ordenada negativa, necesariamente, tiene que haber un valor de abscisa que le corresponda una ordenada nula. Dicho en otras palabras, para que la función tenga un parte por arriba del eje horizontal y otra debajo de este, es porque en algún momento se corta con dicho eje.
Hipótesis:
\( f \) es una función continua dentro de un intervalo \( [a,b] \)
\( f(a)·f(b)<0 \)
Tesis:
Existe al menos un \( c,c∈[a,b] / f( c ) = 0 \)
Demostración:
Se realiza a través del concepto de supremo de un conjunto.

\( f \) es una función continua dentro de un intervalo \( [a,b] \)
\( f(a)·f(b)<0 \)
Tesis:
Existe al menos un \( c,c∈[a,b] / f( c ) = 0 \)
Demostración:
Se realiza a través del concepto de supremo de un conjunto.

Cita
A tener en cuenta: que se cumpla la hipótesis del teorema de Bolzano significa que la función tiene al menos una raíz dentro del intervalo estudiado. Si no se cumple la hipótesis del teorema de Bolzano, no significa que no tenga raíces dentro del intervalo estudiado, simplemente no podemos saberlo por este método, es recomendable ver el ejemplo, para entender más.
Veamos si se cumplen las hipótesis del teorema de Bolzano:
· Por ser una función polinómica, sabemos que es continua.
· Estudiaremos los valores funcionales que toma para los extremos del intervalo.
$$ f(-2) = (-2)^3 - 9·(-2) = +10 $$
$$ f(4) = (4)^3 - 9·(4) = +28 $$
Como los valores funciones para ambos extremos, son de igual signo, no podemos afirmar (por el teorema de Bolzano) que la función tiene raíces dentro del intervalo estudiado.
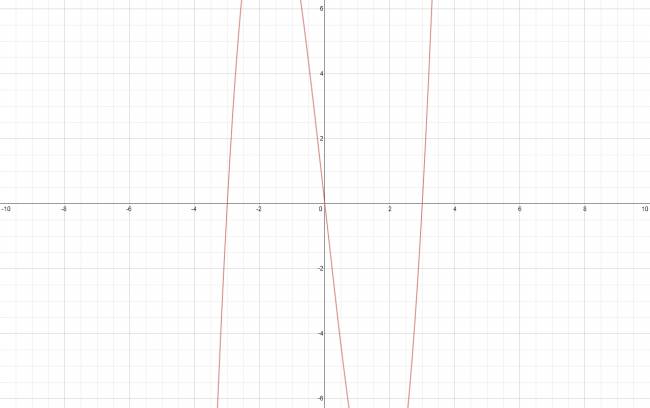
Sin embargo, la función presenta dos raíces dentro de dicho intervalo. En efecto, su conjunto solución, es el siguiente:
$$ S = \left\{ 0, 3, -3 \right\} $$
Y para que no dudemos, dejo también su gráfico:
Código
Estudiar si la función \( f(x) = x^3 - 9·x \), tiene raíces en el intervalo \( [-2,-1] \).
Veamos si se cumplen las hipótesis del teorema de Bolzano:
· Por ser una función polinómica, sabemos que es continua.
· Estudiaremos los valores funcionales que toma para los extremos del intervalo.
$$ f(-2) = (-2)^3 - 9·(-2) = +10 $$
$$ f(4) = (4)^3 - 9·(4) = +28 $$
Como los valores funciones para ambos extremos, son de igual signo, no podemos afirmar (por el teorema de Bolzano) que la función tiene raíces dentro del intervalo estudiado.
Sin embargo, la función presenta dos raíces dentro de dicho intervalo. En efecto, su conjunto solución, es el siguiente:
$$ S = \left\{ 0, 3, -3 \right\} $$
Y para que no dudemos, dejo también su gráfico: