Universo Científico :: Geometría analítica: desdoblada de la tangente

Página 1 de 1
1

Geometría analítica: desdoblada de la tangente

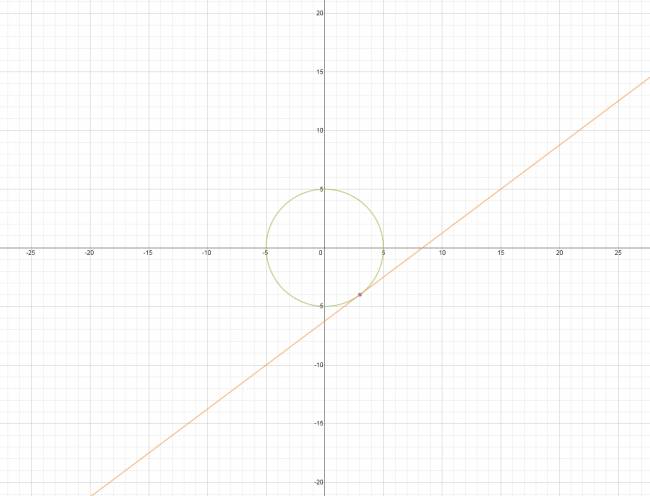
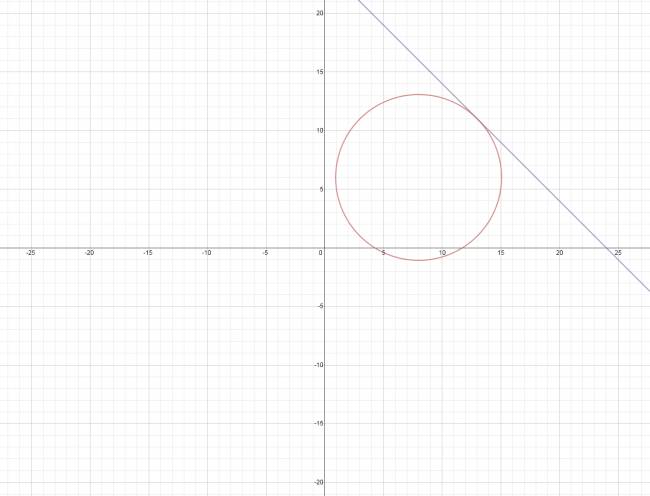
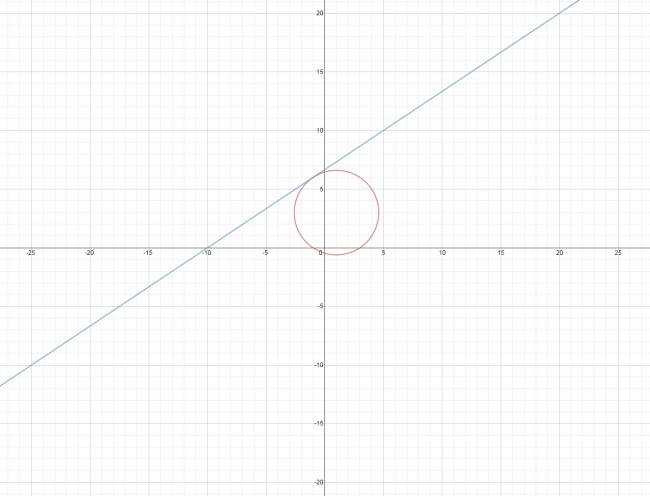
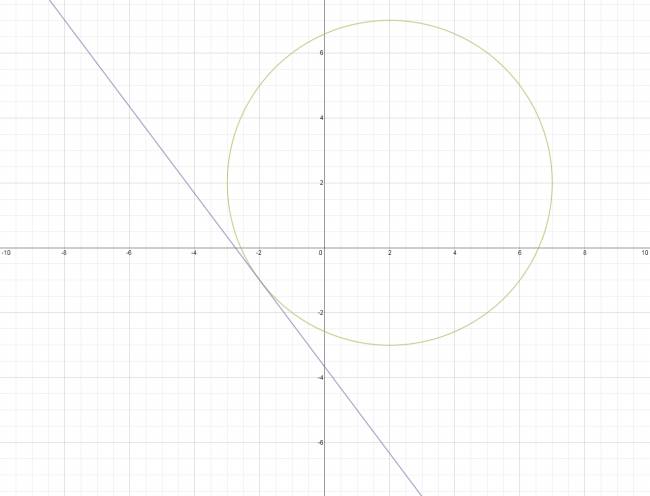
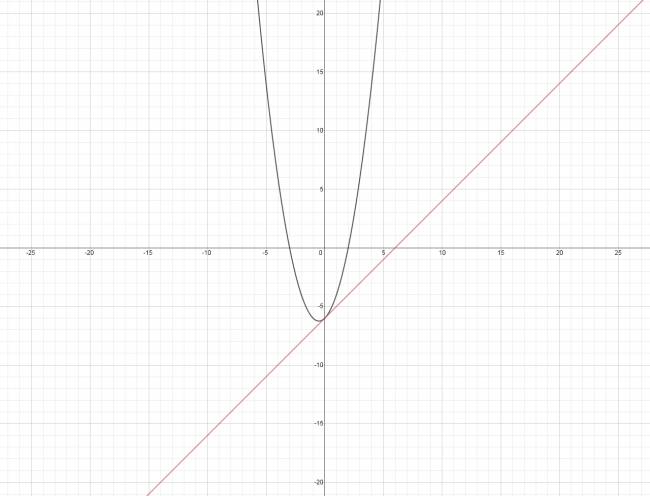
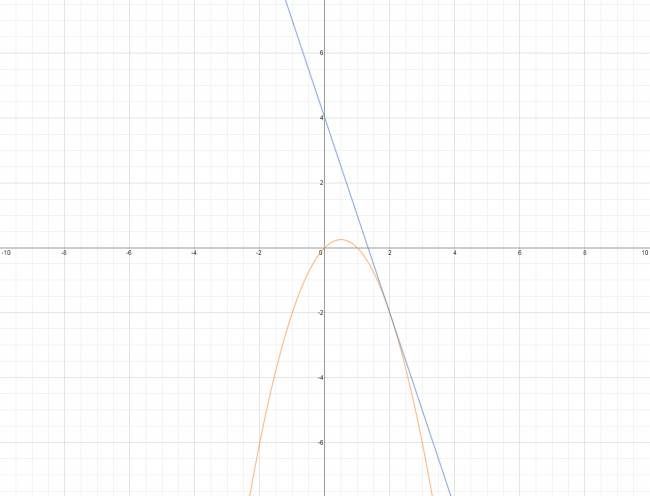
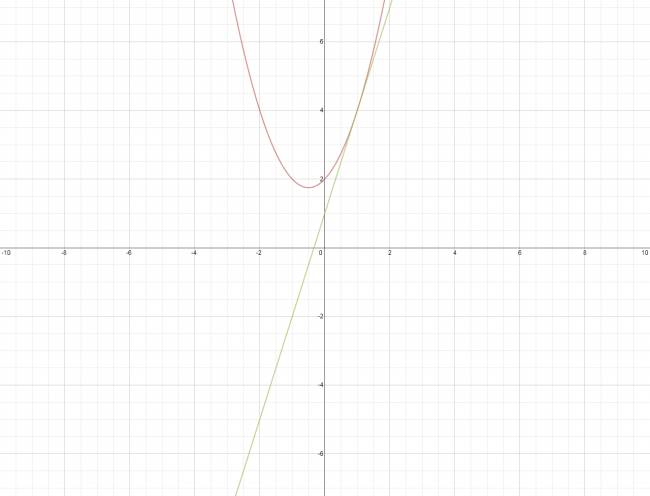
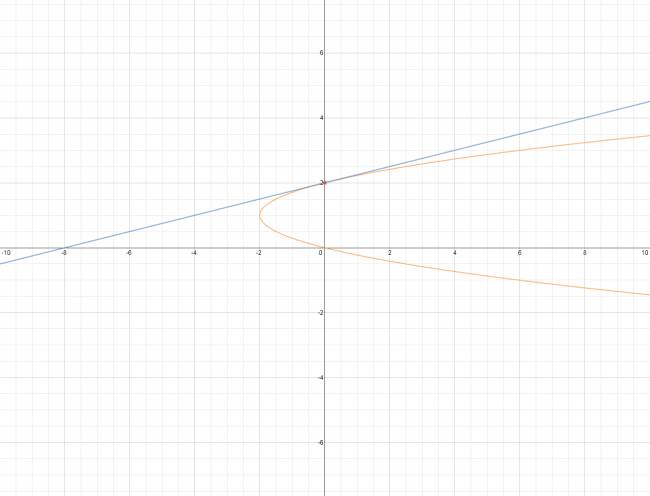
En geometría analítica, la desdoblada de la tangente son un conjunto de cambios que se pueden realizar en cualquiera de las ecuaciones de una cónica (circunferencia, parábola, elipse e hipérbola), dando de esta forma, la ecuación de la recta tangente a la figura en un punto de ella.

Cita

Cambios a realizar:
$$ x^2 → x·x_{o} $$
$$ y^2 → y·y_{o} $$
$$ x·y → \frac {x·y_{o} + x_{o}·y}{2} $$
$$ x → \frac {x+x_{o}}{2} $$
$$ y → \frac {y+y_{o}}{2} $$

Siendo $ P(x_{o},y_{o}) $ el punto de tangencia de la recta con la cónica.

Ejemplos aplicados a cfas y parábolas:

Deducción de los cambios de la desdoblada de la tangente

Primera parte: ecuación de la tangente a una cónica por el origen
La ecuación de una cónica cualquiera es de la forma: $ A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 $. Como pasa por el origen, necesariamente $ F = 0 ⇒ A·x^2 + B·x·y + C·y^2 + D·x + E·y = 0 $

Como la ecuación de la recta tangente pasará por el origen, será de la forma $ (t) y = m·x $. Se reemplaza en la ecuación de la cónica y se ordena en función de $ x $.

$$ (C·m^2 + B·m + A)·x^2 + (D + E·m)·x = 0 $$

Estamos buscando el valor de $ m $ para que $ (t) $ sea tangente a la cónica, por lo tanto, debe tener una única raíz. Es decir, su discriminante debe ser 0.
$$ \Delta = (D + E·m)^2 - 4·(C·m^2 + B·m + A)·0 = 0 ⇒ D + E·m = 0 ⇒ m = - \frac {D}{E}, E≠0 $$

Por lo tanto: $ (t) y = - \frac {D}{E}·x ⇒ (t) D·x + E·y = 0 $. En el caso en que $ E = 0 ⇒ (t) x = 0 $.

Segunda parte: generalización de la ecuación de la tangente a una cónica por cualquier punto de ella
Se realiza una traslación de ejes.

Página 1 de 1
1

Universo Científico

Admin

Admin

Admin