27-08-2013, 10:37 PM
Asíntotas de una función
Definición:
Una asíntota es una recta, a la cual se acerca infinitamente la función. Existen tres tipos de asíntotas.
Tipos de asíntotas:
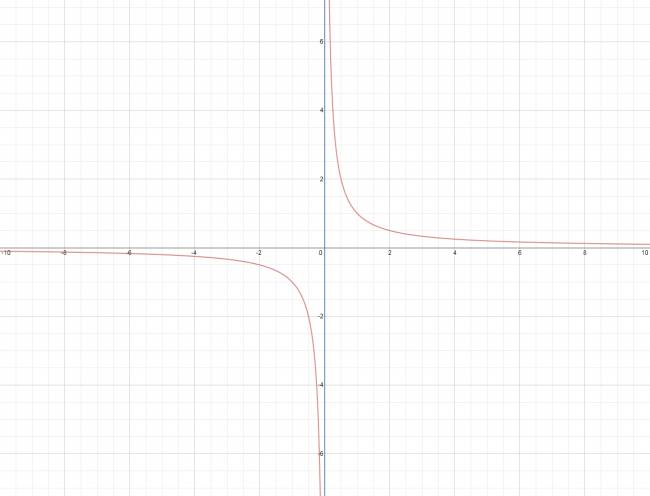
· Asíntota vertical:
Existe una asíntota en \( x = a \) si y sólo si al menos uno de los límites laterales de cuando \( x \to a \) es infinito.
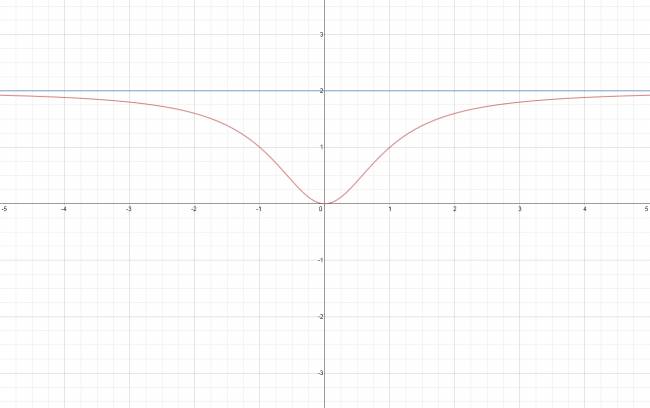
· Asíntota horizontal:
Existe una asíntota en \( y = a \) si y sólo si al menos uno de los límites cuando \( x \to ∞ \) es un número finito \( a \).
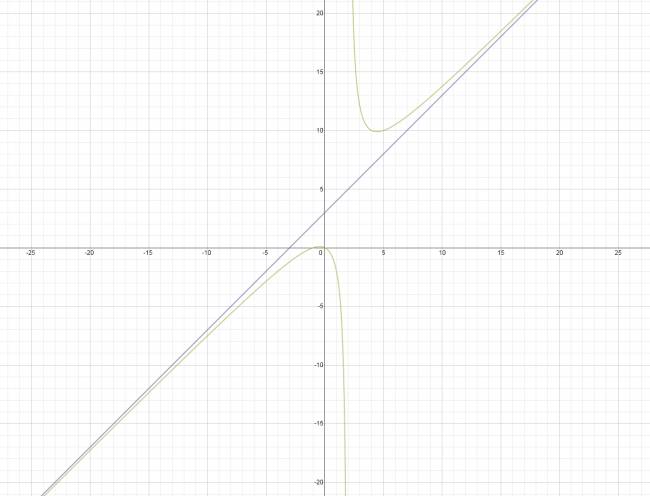
· Asíntota oblicua:
Existe una asíntota oblicua de ecuación \( y = m·x+n \) si y sólo si al menos uno de los límites cuando \( x \to ∞ \) es \( ∞ \).
Cálculo de la asíntota oblicua de ecuación \( y = m·x + n \):
· Cálculo de \( m \):
$$ \lim_{x \to ∞} \frac {f(x)}{x} = m $$
· Cálculo de \( n \):
$$ \lim_{x \to ∞} (f(x) - m·x) = n $$
Con respecto a las asíntotas oblicuas, se debe evaluar el límite para cuando \( x \to +∞ \) y para cuando \( x \to -∞ \), esto se debe a que no siempre coinciden dichas asíntotas. Puede ser que la función presente dos asíntotas oblicuas distintas.
Definición:
Una asíntota es una recta, a la cual se acerca infinitamente la función. Existen tres tipos de asíntotas.
Tipos de asíntotas:
· Asíntota vertical:
Existe una asíntota en \( x = a \) si y sólo si al menos uno de los límites laterales de cuando \( x \to a \) es infinito.
· Asíntota horizontal:
Existe una asíntota en \( y = a \) si y sólo si al menos uno de los límites cuando \( x \to ∞ \) es un número finito \( a \).
· Asíntota oblicua:
Existe una asíntota oblicua de ecuación \( y = m·x+n \) si y sólo si al menos uno de los límites cuando \( x \to ∞ \) es \( ∞ \).
Cálculo de la asíntota oblicua de ecuación \( y = m·x + n \):
· Cálculo de \( m \):
$$ \lim_{x \to ∞} \frac {f(x)}{x} = m $$
· Cálculo de \( n \):
$$ \lim_{x \to ∞} (f(x) - m·x) = n $$
Con respecto a las asíntotas oblicuas, se debe evaluar el límite para cuando \( x \to +∞ \) y para cuando \( x \to -∞ \), esto se debe a que no siempre coinciden dichas asíntotas. Puede ser que la función presente dos asíntotas oblicuas distintas.