24-08-2013, 6:45 AM
Hallar las ecuaciones de las medianas de un triángulo y su baricentro (g)
Una mediana es una semirrecta que se origina en un punto (un vértice) y corta en el punto medio del segmento formado por los otros dos puntos (otros dos vértices del triángulo).
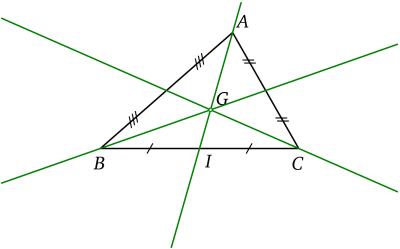
· Ecuación de la mediana que pasa por A y el punto medio de BC:
$$ (y-y_{A})·(2·x_{A}-x_{B}-x_{C})=(x-x_{A})·(2·y_{A}-y_{B}-y_{C}) $$
· Ecuación de la mediana que pasa por B y el punto medio de AC:
$$ (y-y_{B})·(2·x_{B}-x_{A}-x_{C})=(x-x_{B})·(2·y_{B}-y_{A}-y_{C}) $$
· Ecuación de la mediana que pasa por C y el punto medio de AB:
$$ (y-y_{C})·(2·x_{C}-x_{A}-x_{B})=(x-x_{C})·(2·y_{C}-y_{A}-y_{B}) $$
El baricentro del triángulo, se puede hallar como sistema de ecuación de las anteriores tres ecuaciones formadas.
Una mediana es una semirrecta que se origina en un punto (un vértice) y corta en el punto medio del segmento formado por los otros dos puntos (otros dos vértices del triángulo).

· Ecuación de la mediana que pasa por A y el punto medio de BC:
$$ (y-y_{A})·(2·x_{A}-x_{B}-x_{C})=(x-x_{A})·(2·y_{A}-y_{B}-y_{C}) $$
· Ecuación de la mediana que pasa por B y el punto medio de AC:
$$ (y-y_{B})·(2·x_{B}-x_{A}-x_{C})=(x-x_{B})·(2·y_{B}-y_{A}-y_{C}) $$
· Ecuación de la mediana que pasa por C y el punto medio de AB:
$$ (y-y_{C})·(2·x_{C}-x_{A}-x_{B})=(x-x_{C})·(2·y_{C}-y_{A}-y_{B}) $$
El baricentro del triángulo, se puede hallar como sistema de ecuación de las anteriores tres ecuaciones formadas.