14-08-2013, 11:15 PM
Potencial eléctrico
Cuando una carga se desplaza entre dos puntos \( A \) y \( B \) de un campo eléctrico, las fuerzas del campo que actúan sobre ella, realizan un trabajo \( W_{AB} \) (léase trabajo realizado por la fuerza \( F_{E} \) desde el punto \( A \) hasta el punto \( B \)).
La fuerza eléctrica \( F_{E} \) es una fuerza conservativa, de esta forma podemos afirmar que sin importar cuál sea la trayectoria desde el punto \( A \) hasta el punto \( B \), el valor de \( W_{AB} \) será siempre el mismo.
Diferencia de potencial eléctrico:
Fórmulas:
Para campos eléctricos uniformes:
$$ \Delta V = -E·\Delta x· cos \alpha $$
Ejemplo de campo eléctrico uniforme:
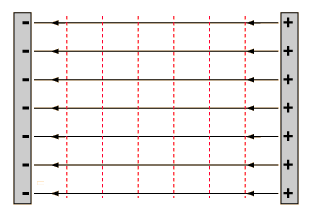
Si me muevo en el sentido del campo eléctrico:
· Si llevo una qo>0 en el sentido de campo, gana Ec y pierde Epe.
· Si llevo una qo<0 en el sentido de campo, pierde Ec y gana Epe.
Para campos eléctricos no-uniformes:
$$ \Delta V = \frac {Epe}{q_{0}} $$
$$ \Delta V = \frac {-W_{F_{E}}}{q_{0}} $$
$$ \Delta V = \frac {-\Delta Ec}{q_{0}} $$
Ejemplo de campo eléctrico no-uniforme:
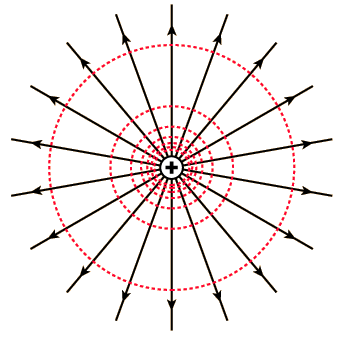
De las anteriores fórmulas, podemos deducir las siguientes igualdades:
\( W_{F_{E}} = \Delta Ec \)
\( W_{F_{E}} = -Epe \)
Referencias:
Unidades:
$$ \Delta V \left [ \frac {J}{C} \right ] $$
Líneas equipotenciales:
Es el lugar físico donde el valor de campo eléctrico es constante.

En la imagen superior, las líneas equipotenciales son las representadas en rojo.
Propiedades:
· Son perpendiculares a las líneas de campo.
· Son paralelas entre sí si el campo eléctrico es uniforme.
· El sentido del campo eléctrico es de las líneas equipotenciales decrecientes.
Potencial eléctrico para una carga:
Es una magnitud escalar.
Fórmula:
$$ V = \frac {k·q}{r} \left [ V \right ] $$
Referencias:
Propiedades:
· El valor del potencial eléctrico de la carga en un punto ubicado a una distancia infinita de esta, es cero: \( V_{∞} = 0 \).
Cuando una carga se desplaza entre dos puntos \( A \) y \( B \) de un campo eléctrico, las fuerzas del campo que actúan sobre ella, realizan un trabajo \( W_{AB} \) (léase trabajo realizado por la fuerza \( F_{E} \) desde el punto \( A \) hasta el punto \( B \)).
La fuerza eléctrica \( F_{E} \) es una fuerza conservativa, de esta forma podemos afirmar que sin importar cuál sea la trayectoria desde el punto \( A \) hasta el punto \( B \), el valor de \( W_{AB} \) será siempre el mismo.
Diferencia de potencial eléctrico:
Fórmulas:
Para campos eléctricos uniformes:
$$ \Delta V = -E·\Delta x· cos \alpha $$
Ejemplo de campo eléctrico uniforme:

Si me muevo en el sentido del campo eléctrico:
· Si llevo una qo>0 en el sentido de campo, gana Ec y pierde Epe.
· Si llevo una qo<0 en el sentido de campo, pierde Ec y gana Epe.
Para campos eléctricos no-uniformes:
$$ \Delta V = \frac {Epe}{q_{0}} $$
$$ \Delta V = \frac {-W_{F_{E}}}{q_{0}} $$
$$ \Delta V = \frac {-\Delta Ec}{q_{0}} $$
Ejemplo de campo eléctrico no-uniforme:

De las anteriores fórmulas, podemos deducir las siguientes igualdades:
\( W_{F_{E}} = \Delta Ec \)
\( W_{F_{E}} = -Epe \)
Referencias:
Unidades:
$$ \Delta V \left [ \frac {J}{C} \right ] $$
Cita
A tener en cuenta la siguiente igualdad:
$$ \frac {V}{m} = \frac {N}{C} $$
Esto es cierto ya que:
$$ \frac {V}{m} = \frac {\frac {J}{C}}{m} = \frac {\frac {N·m}{C}}{m} = \frac {N}{C} $$
$$ \frac {V}{m} = \frac {N}{C} $$
Esto es cierto ya que:
$$ \frac {V}{m} = \frac {\frac {J}{C}}{m} = \frac {\frac {N·m}{C}}{m} = \frac {N}{C} $$
Líneas equipotenciales:
Es el lugar físico donde el valor de campo eléctrico es constante.

En la imagen superior, las líneas equipotenciales son las representadas en rojo.
Propiedades:
· Son perpendiculares a las líneas de campo.
· Son paralelas entre sí si el campo eléctrico es uniforme.
· El sentido del campo eléctrico es de las líneas equipotenciales decrecientes.
Potencial eléctrico para una carga:
Es una magnitud escalar.
Fórmula:
$$ V = \frac {k·q}{r} \left [ V \right ] $$
Referencias:
Propiedades:
· El valor del potencial eléctrico de la carga en un punto ubicado a una distancia infinita de esta, es cero: \( V_{∞} = 0 \).