Universo Científico :: Lugar geométrico, analítica, rectas

Página 1 de 1
1

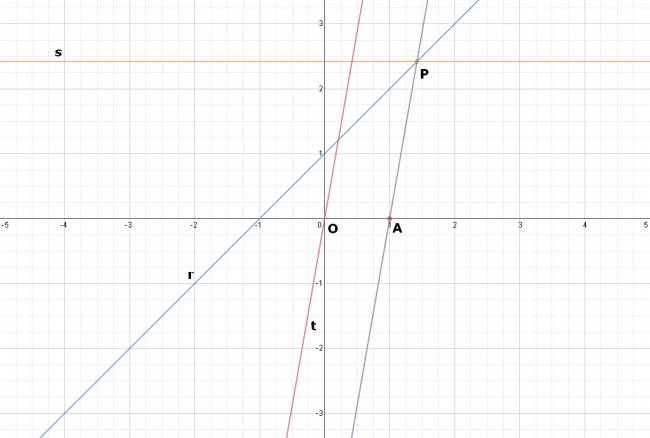
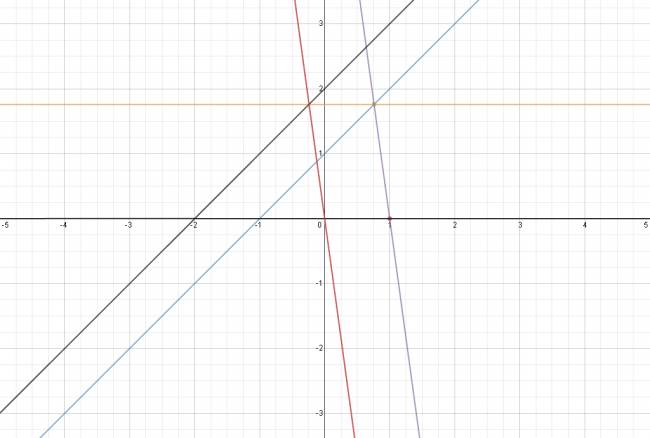
Sea la recta $ ( r ) y = x + 1 $, donde $ P $ es un punto variable en $ ( r ) $. Sea $ A (1, 0) $.
Se sabe que $ ( s ) || O \vec x $ por $ P $. $ (t) || AP $ por $ O (0, 0) $.

Hallar el lugar geométrico de $ s∩t $.

Graficamos lo que conocemos:

Ahora viene lo divertido: hallar las ecuaciones de todas las rectas y hallar las coordenadas de todos los puntos.

Se deduce de la recta $ ( r ) $ que: $ P (a, a+1) ⇒ ( s ) y = a + 1 $

Calculamos la recta $ AP $ por la fórmula de "recta que pasa por dos puntos", pero sólo nos interesa su pendiente:
$$ m_{AP} = \frac {a+1}{a-1}, a≠1 $$

Entonces la recta $ (t) $ tendrá la misma pendiente y no tendrá término independiente en su ecuación:
$$ (t) y = \frac {a+1}{a-1}·x $$

Se me pedía el lugar geométrico de $ s ∩ t $ por lo que de ahora en más sólo me interesarán sus ecuaciones:

$$ (s) y = a + 1 ⇒ (s) a = y - 1 $$

Reemplazamos en la ecuación de $ (t) $.

$$ (t) y = \frac {a+1}{a-1}·x ⇒ (t) y = \frac {y - 1+1}{y - 1 -1}·x ⇒ (t) y = \frac {y}{y - 2}·x $$

Despejamos y obtenemos el lugar geométrico buscado, que es un producto de rectas:
$$ y·(y-x-2) = 0 $$

Se representa el lugar geométrico con color negro:

Página 1 de 1
1

Universo Científico

marcos364

Admin