20-06-2013, 0:32 AM
- Página 1 de 1
- 1
| Foro Problemas resueltos Estudio de funciones logarítimicas en valor absoluto |
| Estudio de funciones logarítimicas en valor absoluto |
20-06-2013, 0:42 AM
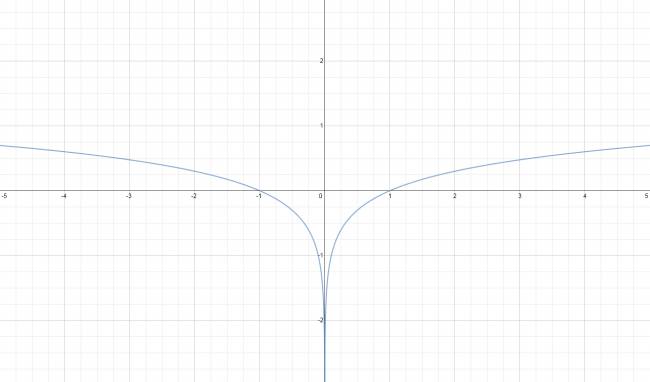
$$ f(x) = \mbox{Ln} |x| $$
Esta función es relativamente fácil de graficar. Sabemos que su raíz es: +1 y la función no existe para: 0. Expresado en forma matemática: $$ S = \left\{ 1 \right\} $$ $$ D = ℝ - \left\{ 0 \right\} $$ Si estudiamos los límites laterales para el punto de no existencia tenemos que: $$ \lim_{x \to 0^{±}} \mbox{Ln} |x| = -∞ $$ Como es igual por derecha y por izquierda, el límite existe en \( x = 0 \). Ahora estudiamos los límites para los extremos: $$ \lim_{x \to ±∞} \mbox{Ln} |x| = +∞ $$ Como es una función en valor absoluto, generalmente tiene un eje de simetría y en este caso es con respecto al eje \( O \vec y \) Finalmente la graficamos:  |
20-06-2013, 0:45 AM
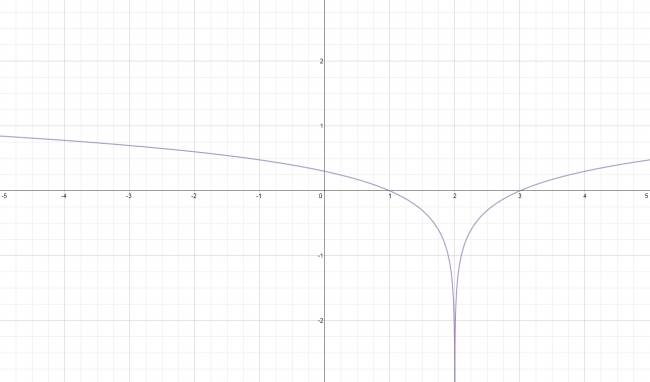
$$ g(x) = \mbox{Ln} |x - 2| $$
Ídem del anterior con un corrimiento de dos unidades hacia la derecha. Ordenada en el origen: $$ g(0) = \mbox{Ln} 2 $$ La graficamos:  |
20-06-2013, 0:56 AM
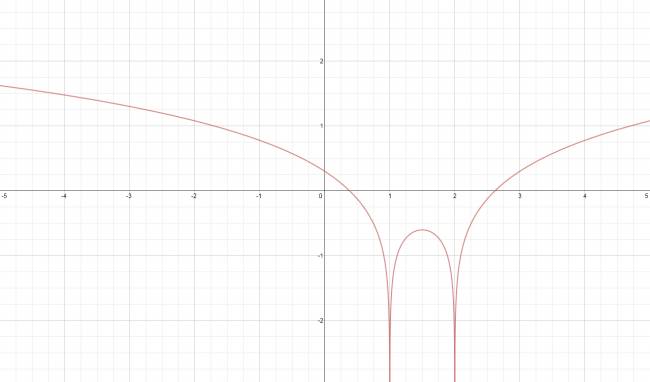
$$ h(x) = \mbox{Ln} |x^2-3·x+2| $$
Hallamos las raíces: Aplicamos la definición de logaritmo y de valor absoluto: $$ \mbox{Ln} |x^2-3·x+2| ⇔ x^2-3·x+2 = ±1 $$ $$ x^2-3·x+2 = +1 → S = \left\{ \frac {3+\sqrt{5}}{2}, \frac {3-\sqrt{5}}{2} \right\} $$ $$ x^2-3·x+2 = -1 → S = ∅ $$ Digo que es conjunto vacío porque estamos trabajando en \( ℝ \). Las raíces de la función son: $$ S = \left\{ \frac {3+\sqrt{5}}{2}, \frac {3-\sqrt{5}}{2} \right\} $$ Ordenada en el origen: $$ h(0) = \mbox{Ln} 2 $$ Hallamos los puntos de inexistencia (asíntotas verticales): $$ x^2-3·x+2 = +1 → S = \left\{ 1, 2 \right\} $$ $$ D = ℝ - \left\{ 1, 2 \right\} $$  |
- Página 1 de 1
- 1