01-06-2013, 9:48 PM
- Página 1 de 1
- 1
| Foro Problemas sin resolver Problemas de cfas, geo analítica, inecuación, sistema, tange |
| Problemas de cfas, geo analítica, inecuación, sistema, tange |
|
01-06-2013, 9:53 PM
1. a.
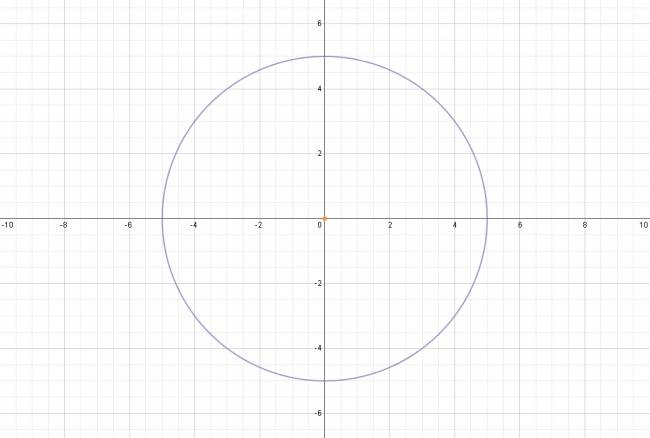
Si se nos dice que el centro se encuentra en el origen, podemos afirmar que los términos de \( x \) y de \( y \) de primer grado, serán nulos, no aparecerán en la ecuación. $$ x^2 + y^2 -2·\alpha·x - 2·\beta·y + \alpha^2 + \beta^2 - r^2 = 0 $$ $$ x^2 + y^2 -2·0·x - 2·0·y + 0^2 + 0^2 - 5^2 = 0 $$ $$ x^2 + y^2 - 25 = 0 $$  |
01-06-2013, 9:55 PM
1. b.
$$ x^2 + y^2 -2·\alpha·x - 2·\beta·y + \alpha^2 + \beta^2 - r^2 = 0 $$ $$ x^2 + y^2 -2·2·x - 2·3·y + 2^2 + 3^2 - 4^2 = 0 $$ $$ x^2 + y^2 - 4·x - 6·y + 4 + 9 - 16 = 0 $$ $$ x^2 + y^2 - 4·x - 6·y -3 = 0 $$  |
01-06-2013, 10:03 PM
1. c.
Cuando se nos dice que la cfa pasa por el origen de coordenadas, podemos afirmar que el término independiente (aquel que no posee variable) es nulo. $$ x^2 + y^2 -2·\alpha·x - 2·\beta·y = 0 $$ $$ x^2 + y^2 -2·(-1)·x - 2·(4)·y = 0 $$ $$ x^2 + y^2 +2·x - 8·y = 0 $$  |
01-06-2013, 10:11 PM
1. d.
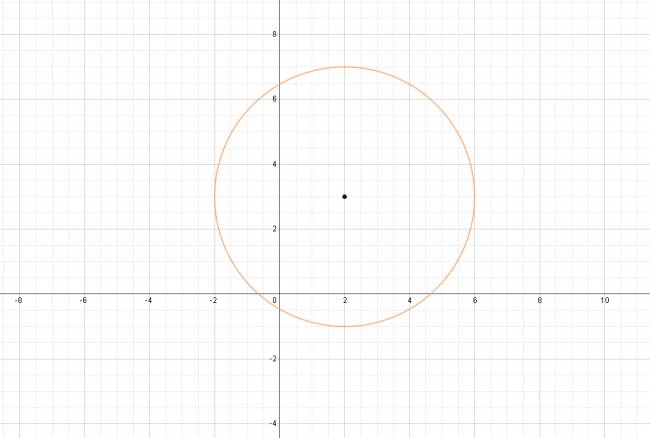
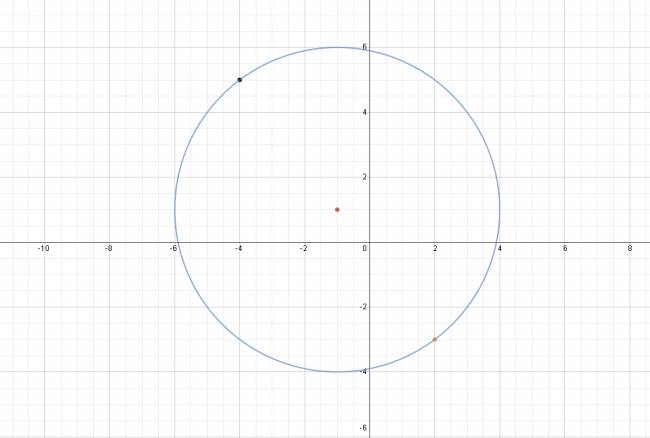
El diámetro de la cfa, es cualquier segmento que pase por el centro de la cfa y cumpla que: \( 2·r = d \). Veamos la siguiente ilustración:  Como podemos apreciar, el punto medio entre los extremos de la cfa es el radio. Conociendo ambos puntos, podemos aplicar "punto medio de un segmento" y calcular el centro de la cfa. Es lo que haremos. $$ C \left ( \frac {2-4}{2}, \frac {-3+5}{2} \right ) ⇒ C \left ( -1, 1 \right ) $$ $$ x^2 + y^2 -2·\alpha·x - 2·\beta·y + \gamma = 0 $$ $$ x^2 + y^2 -2·(-1)·x - 2·(1)·y + \gamma = 0 $$ $$ x^2 + y^2 +4·x - 2·y + \gamma = 0 $$ Sustituimos por las coordenadas de cualquiera de los dos puntos: $$ (2)^2 + (-3)^2 +4·(2) - 2·(-3) + \gamma = 0 $$ $$ 4 + 9 +8 +6 + \gamma = 0 ⇒ \gamma = -23 $$ $$ x^2 + y^2 +4·x - 2·y - 23 = 0 $$  |
01-06-2013, 10:44 PM
1. e.
$$ x^2 + y^2 -2·\alpha·x - 2·\beta·y + \gamma = 0 $$ $$ x^2 + y^2 -2·(-1)·x - 2·(2)·y + \gamma = 0 $$ $$ x^2 + y^2 + 2·x - 4·y + \gamma = 0 $$ Reemplazamos las coordenadas del punto: $$ (2)^2 + (6)^2 + 2·(2) - 4·(6) + \gamma = 0 ⇒ \gamma = -20 $$ $$ x^2 + y^2 + 2·x - 4·y -20 = 0 $$  |
01-06-2013, 10:53 PM
1. f.
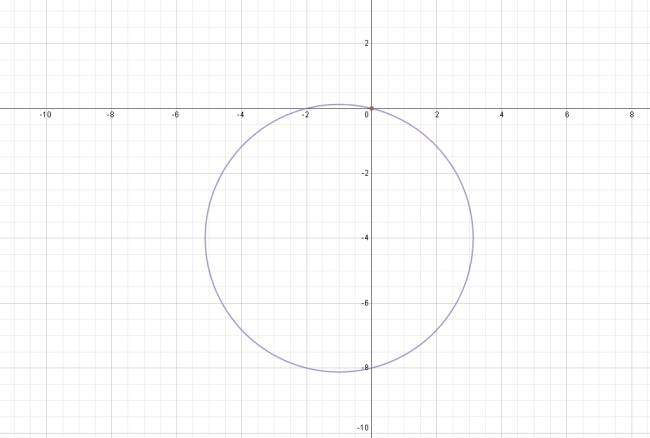
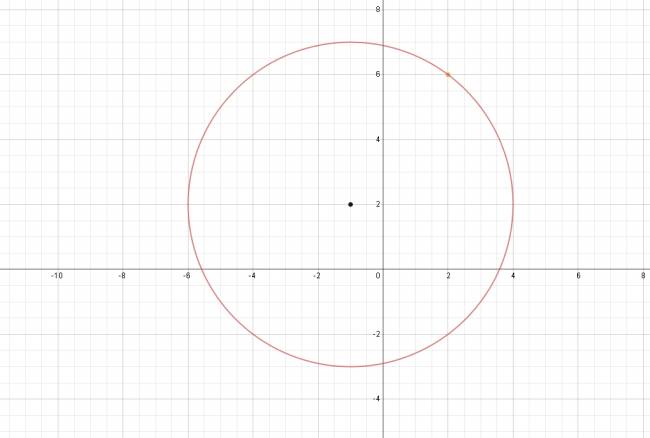
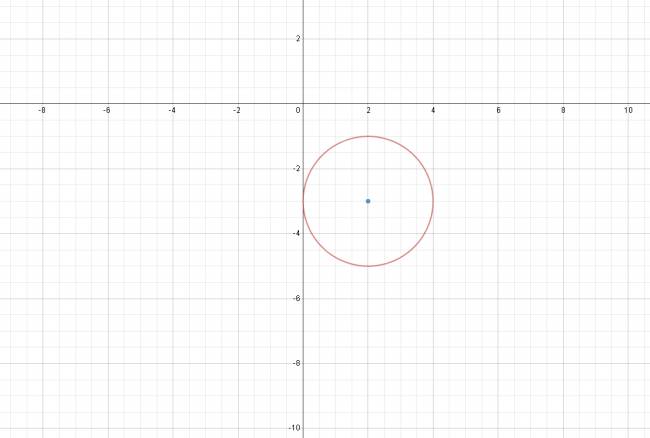
Cita A tener en cuenta: Si se nos dice que la cfa es tangente al eje \( O \vec y \), entonces, el radio será igual a la abscisa del centro. Si se nos dice que la cfa es tangente al eje \( O \vec x \), entonces, el radio será igual a la ordenada del centro. Por lo que podemos afirmar que el radio es \( r = 2 \). $$ x^2 + y^2 -2·(2)·x - 2·(-3)·y + (2)^2 + (-3)^2 - (2)^2 = 0 $$ $$ x^2 + y^2 -4·x + 6·y + 4 + 9 - 4 = 0 $$ $$ x^2 + y^2 -4·x + 6·y + 9 = 0 $$  |
01-06-2013, 11:27 PM
2. a.
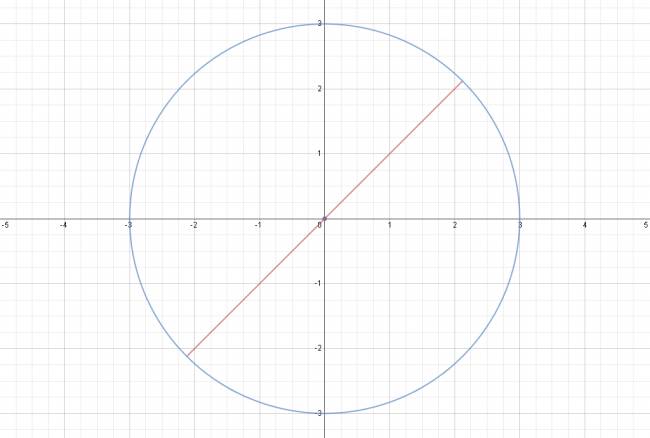
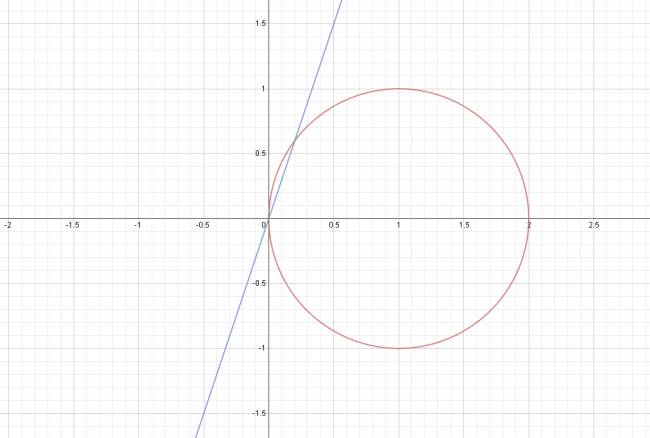
$$ \begin{cases} x^2 + y^2 - 2·x = 0 \\ y = 3·x \end{cases} $$ $$ x^2 + y^2 - 2·x = 0 ⇒ x^2 + (3·x)^2 - 2·x = 0 ⇒ x^2 + 9·x^2 - 2·x = 0 ⇒ 10·x^2 - 2·x = 0 ⇒ 5·x^2 - x = 0 $$ $$ 5·x^2 - x = 0 ⇒ x·(5·x -1) = 0 ⇔ x = 0 v 5·x -1 = 0 $$ $$ \left\{ 0, \frac {1}{5} \right\} $$ · Cuando \( x = 0 \): $$ y = 3·0 ⇒ y = 0 $$ $$ A (0,0) $$ · Cuando \( x = \frac {1}{5} \): $$ y = 3·\frac {1}{5} ⇒ y = \frac {3}{5} $$ $$ B \left (\frac {1}{5},\frac {3}{5}\right ) $$ Son secantes en: $$ S = \left\{ (0,0); \left (\frac {1}{5},\frac {3}{5}\right ) \right\} $$  |
- Página 1 de 1
- 1