30-05-2013, 0:02 AM
Geometría analítica: hallar el cuarto vértice de un cuadrado conociendo los tres restantes, de forma analítica, aplicando fórmulas
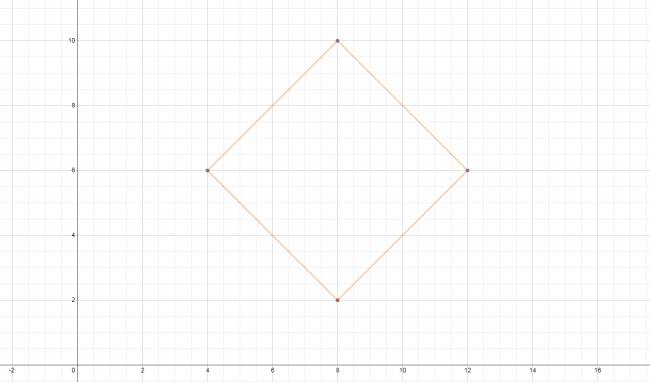
Supongamos que conocemos los puntos violetas y queremos hallar el punto rojo, como vemos, los cuatro puntos forman un cuadrado.
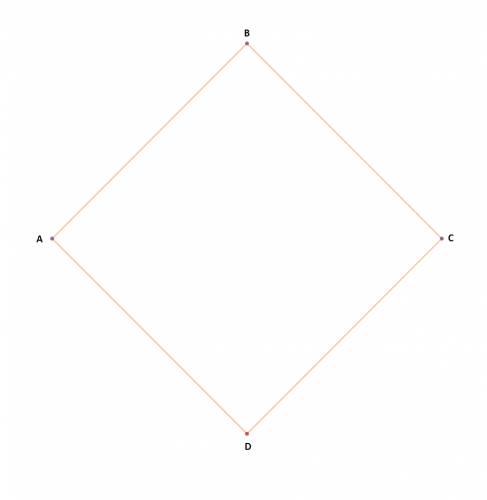
Antes de ver las fórmulas, acordemos el orden de los puntos:
Ahora estamos en condiciones de ver las fórmulas:
\( D(x_{D}, y_{D}) \)
$$ x_{D} = x_{A} - x_{B} + x_{C} $$
$$ y_{D} = y_{A} - y_{B} + y_{C} $$
Como vemos, para calcular la abscisa del punto es cuestión, debemos sumar las abscisas de los puntos de la diagonal opuesta, y restar la del vértice opuesto. Se procede análogamente para calcular la ordenada.
Supongamos que conocemos los puntos violetas y queremos hallar el punto rojo, como vemos, los cuatro puntos forman un cuadrado.
Antes de ver las fórmulas, acordemos el orden de los puntos:
Ahora estamos en condiciones de ver las fórmulas:
\( D(x_{D}, y_{D}) \)
$$ x_{D} = x_{A} - x_{B} + x_{C} $$
$$ y_{D} = y_{A} - y_{B} + y_{C} $$
Como vemos, para calcular la abscisa del punto es cuestión, debemos sumar las abscisas de los puntos de la diagonal opuesta, y restar la del vértice opuesto. Se procede análogamente para calcular la ordenada.