28-05-2013, 0:31 AM
Geometría analítica: hallar vértices de un triángulo conociendo el punto medio de cada uno de sus lados
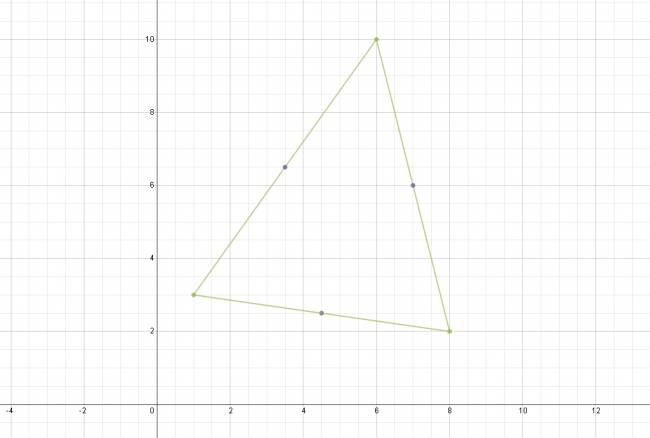
Supongamos que se conocen los puntos violetas y se quiere conocer los vértices del triángulo verde:
Para esto utilizaremos las siguientes fórmulas, deducidas por mí.
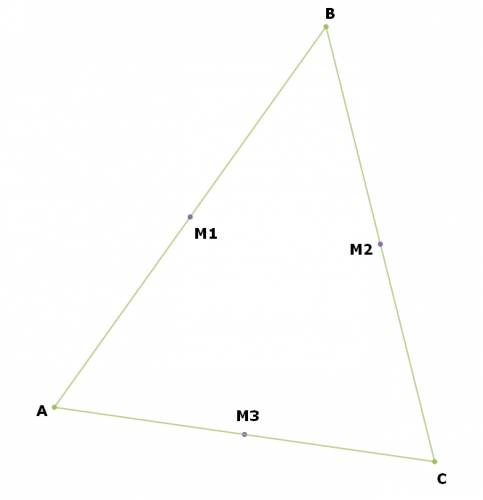
Antes de ver las fórmulas, es conveniente acordar las referencias de cada punto, no importa el orden en que se enumeren, pero debe ser el mismo ciclo que muestro a continuación:
Para hallar A:
\( A(x_{A}, y_{A}) \)
\( x_{A} = x_{M1} - x_{M2} + x_{M3} \)
\( y_{A} = y_{M1} - y_{M2} + y_{M3} \)
Para hallar B:
\( B(x_{B}, y_{B}) \)
\( x_{B} = x_{M1} + x_{M2} - x_{M3} \)
\( y_{B} = x_{M1} + x_{M2} - x_{M3} \)
Para hallar C:
\( C(x_{C}, y_{C}) \)
\( x_{C} = -x_{M1} + x_{M2} + x_{M3} \)
\( y_{C} = -y_{M1} + y_{M2} + y_{M3} \)
Supongamos que se conocen los puntos violetas y se quiere conocer los vértices del triángulo verde:
Para esto utilizaremos las siguientes fórmulas, deducidas por mí.
Antes de ver las fórmulas, es conveniente acordar las referencias de cada punto, no importa el orden en que se enumeren, pero debe ser el mismo ciclo que muestro a continuación:
Para hallar A:
\( A(x_{A}, y_{A}) \)
\( x_{A} = x_{M1} - x_{M2} + x_{M3} \)
\( y_{A} = y_{M1} - y_{M2} + y_{M3} \)
Para hallar B:
\( B(x_{B}, y_{B}) \)
\( x_{B} = x_{M1} + x_{M2} - x_{M3} \)
\( y_{B} = x_{M1} + x_{M2} - x_{M3} \)
Para hallar C:
\( C(x_{C}, y_{C}) \)
\( x_{C} = -x_{M1} + x_{M2} + x_{M3} \)
\( y_{C} = -y_{M1} + y_{M2} + y_{M3} \)