18-05-2013, 1:12 AM
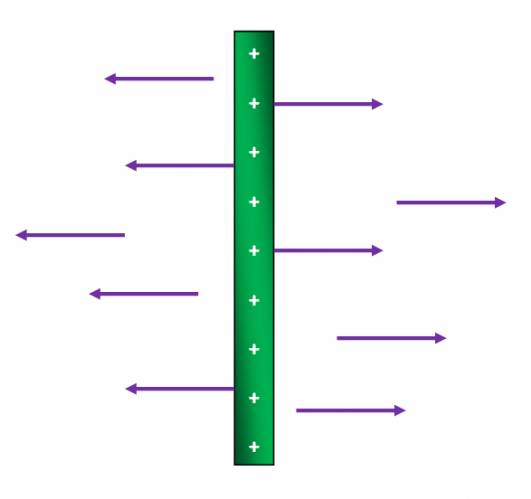
Flujo eléctrico
Expresión matemática:
$$ \Phi_{E} = E·S·\cos \alpha \left [ \frac {N·m^2}{C} \right ] $$
Referencias:
\( \alpha \) es el ángulo formado entre el vector campo eléctrico (E) y el vector superficie (que es perpendicular a la superficie).
Expresión matemática:
$$ \Phi_{E} = E·S·\cos \alpha \left [ \frac {N·m^2}{C} \right ] $$
Referencias:
\( \alpha \) es el ángulo formado entre el vector campo eléctrico (E) y el vector superficie (que es perpendicular a la superficie).