14-05-2013, 11:29 PM
Familia de rectas
Definición:
Es un conjunto de rectas que cumplen una cierta condición.
Como ya sabremos, una recta es de la forma \( y = m·x + n \) o \( a·x + b·y + c = 0 \). Cuando hablamos de una familia de rectas, estamos hablando de una ecuación paramétrica de la recta. Las variables \( x \) e \( y \) deben ser de primer grado (de lo contrario no sería una recta). No, no es tan nueva la cosa. Mirá un ejemplo:
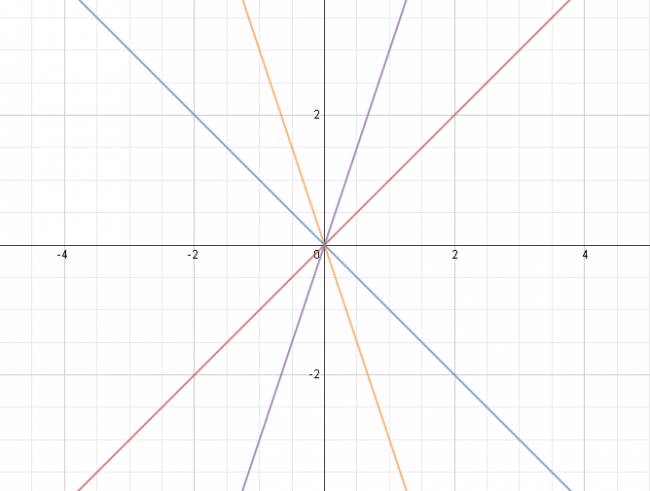
$$ y = a·x $$
Si decimos que \( a ∈ ℕ \), para cada valor de \( a \) voy a tener una recta.
Recordemos que si nos basamos en geometría euclidiana: infinitas rectas pasan por un mismo punto, por lo que en el caso anterior, habrán tantas rectas que pasen por ese punto como números reales hay (hay infinitos números reales).
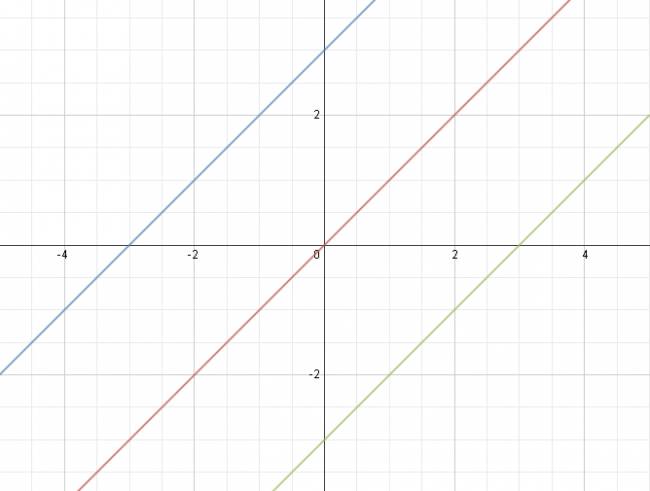
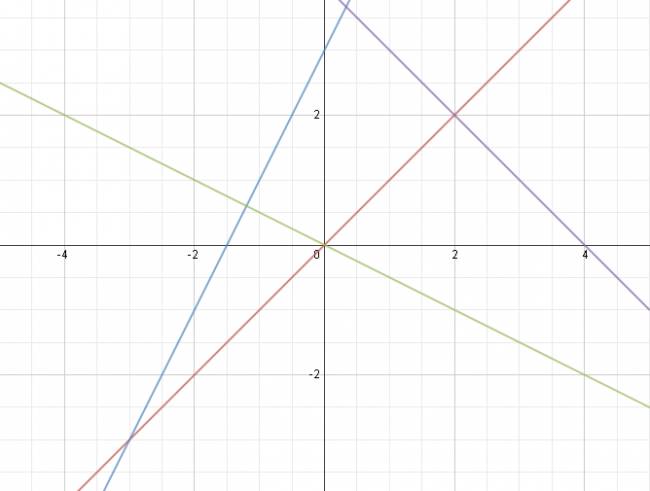
Pero hay más complejas:
$$ y = (k + 8)·x + k - 2 $$
$$ y = 2·b·x - b $$
$$ y = (h^2 + 3·h - 2)·x + 4·h $$
$$ (s + 2)·x + (4·s + 1)·y + s - 2 = 0 $$
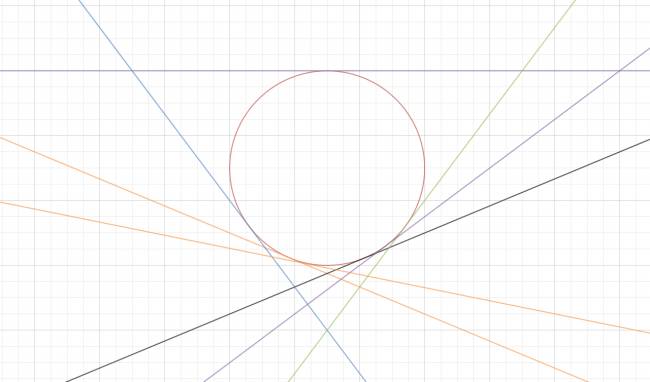
Ya te veo preguntándote, y ¿qué tipos de ejercicios me pueden preguntar sobre esto? Bueno, todo iba muy lindo, pero ahora la cosa es saber si esas ecuaciones forman o no un haz, y si lo hacen, cómo es. O hallar la familia de rectas que pasan por un punto, etc.
Definición:
Es un conjunto de rectas que cumplen una cierta condición.
Como ya sabremos, una recta es de la forma \( y = m·x + n \) o \( a·x + b·y + c = 0 \). Cuando hablamos de una familia de rectas, estamos hablando de una ecuación paramétrica de la recta. Las variables \( x \) e \( y \) deben ser de primer grado (de lo contrario no sería una recta). No, no es tan nueva la cosa. Mirá un ejemplo:
$$ y = a·x $$
Si decimos que \( a ∈ ℕ \), para cada valor de \( a \) voy a tener una recta.
Recordemos que si nos basamos en geometría euclidiana: infinitas rectas pasan por un mismo punto, por lo que en el caso anterior, habrán tantas rectas que pasen por ese punto como números reales hay (hay infinitos números reales).
Cita
Un parámetro está representado por una letra del alfabeto latino o griego que no sea \( x \) ni \( y \).
Pero hay más complejas:
$$ y = (k + 8)·x + k - 2 $$
$$ y = 2·b·x - b $$
$$ y = (h^2 + 3·h - 2)·x + 4·h $$
$$ (s + 2)·x + (4·s + 1)·y + s - 2 = 0 $$
Ya te veo preguntándote, y ¿qué tipos de ejercicios me pueden preguntar sobre esto? Bueno, todo iba muy lindo, pero ahora la cosa es saber si esas ecuaciones forman o no un haz, y si lo hacen, cómo es. O hallar la familia de rectas que pasan por un punto, etc.