|
Resolver sistema de ecuaciones de 2x2 por 4 métodos distinto
|
|
Resolver el siguiente sistema de ecuaciones:
$$ \begin{cases} 9·x + y = 90 \\ 15·x - 2·y = -15 \end{cases} $$
Por los métodos de: igualación, sustitución, reducción, y gráfico.
|
Cita (marcos364) igualación
Voy a despejar \( y \):
$$ 9·x + y = 90 ⇒ y = -9·x + 90 $$
$$ 15·x - 2·y = -15 ⇒ y = \frac {15·x + 15}{2} $$
$$ -9·x + 90 = \frac {15·x + 15}{2} $$ |
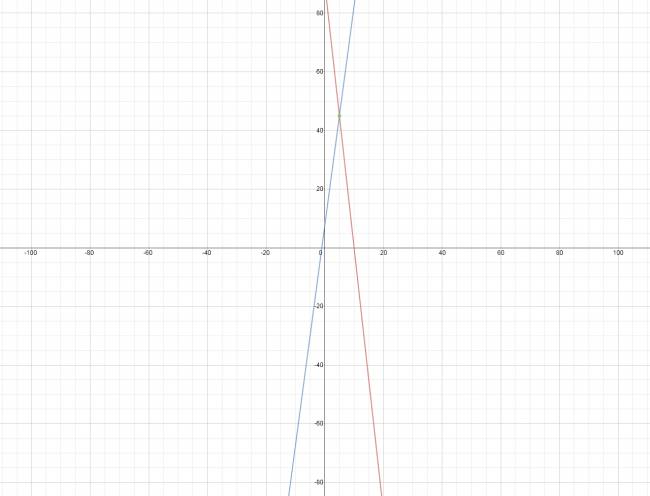
Se grafican ambas ecuaciones, el punto de corte de ambas en el gráfico, es la solución del sistema. Siendo la abscisa el valor de \( x \) y la ordenada el valor de \( y \).
$$ x = 5 ∧ y = 45 $$
|
Cita (marcos364) sustitución |
Cita (marcos364) reducción |