|
Límite de una función
|
|
Límite de una función
Explicación:
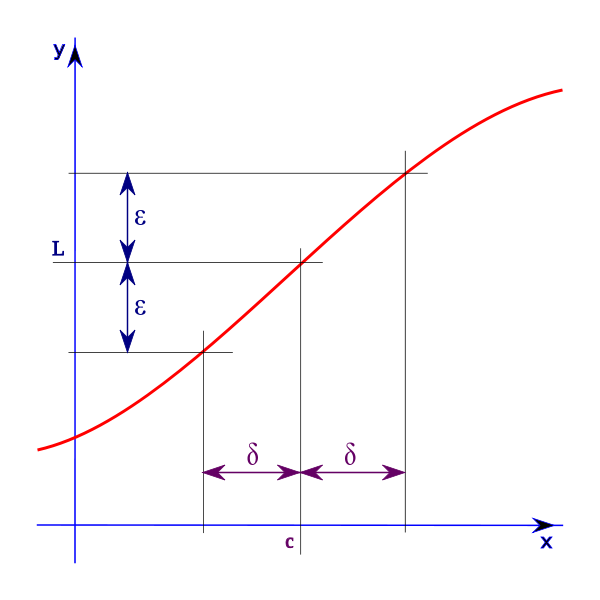
El límite de una función \( f(x) \), cuando \( x \to a \), es el estudio de los valores funcionales, muy cerca de \( x = a \), pero nunca de este valor.
|
Límite finito:
Notación:
$$ \lim_{x \to a} f(x) = b $$
Definición:
$$ \lim_{x \to c} f(x) = L ⇔ ∀ε>0,∃δ>0/\mbox{si }x∈E_{(c,δ)}^{*} ⇒ f(x) ∈E_{(L,ε)} $$
· Condición de existencia del límite finito:
Existe el límite de una función cuando tiende a un número finito, si y sólo si sus límites laterales para dicho valor estudiado, son iguales.
$$ ∃\lim_{x \to a} f(x) ⇔ \lim_{x \to a^{+}} f(x) = \lim_{x \to a^{-}} f(x) $$
|
Teoremas de los límites finitos:
Teorema de unicidad del límite:
Enunciado:
Si el límite de una función existe, es único.
Teorema de conservación del signo:
Enunciado:
Para valores de \( x \) suficientemente próximos al valor de tendencia, la función tiene el mismo signo que su límite.
Teorema de la función comprendida:
Enunciado:
Si los valores de una función están comprendidos entre los de otras dos que tienen igual límite para \( x \to a \), entonces la función tiene el mismo límite.
Teorema fundamental en el cálculo de límites:
Enunciado:
Una función tiene límite finito si y sólo si el límite por la izquierda es igual al límite por la derecha.
Propiedades de los límites finitos:
Límite de la suma:
Enunciado:
El límite de una suma es igual a la suma de los límites de cada término, siempre que estos límites sean finitos.
Límite del producto:
Enunciado:
El límite de un producto es igual al producto de los límites de cada factor, siempre que estos límites sean finitos.
Límite de un cociente:
Enunciado:
El límite de un cociente es igual al cociente de los límites de cada factor, siempre que estos límites sean finitos y el límite del denominador sea distinto de cero.
|
Límites laterales:
Los límites laterales de una función en un punto de esta, nos permite conocer por qué valor nos acercamos, si por valores menores o por mayores.
Esto es muy importante cuando, por ejemplo, el resultado de un límite nos da 0. ¿Nos acercamos por valores positivos o negativos al cero? Esto lo podremos averiguar calculando sus límites laterales.
Límite lateral derecho:
$$ \lim_{x \to a^+} f(x) = b $$
Límite lateral izquierdo:
$$ \lim_{x \to a^-} f(x) = b $$
Ahora supongamos la siguiente función ejemplo:
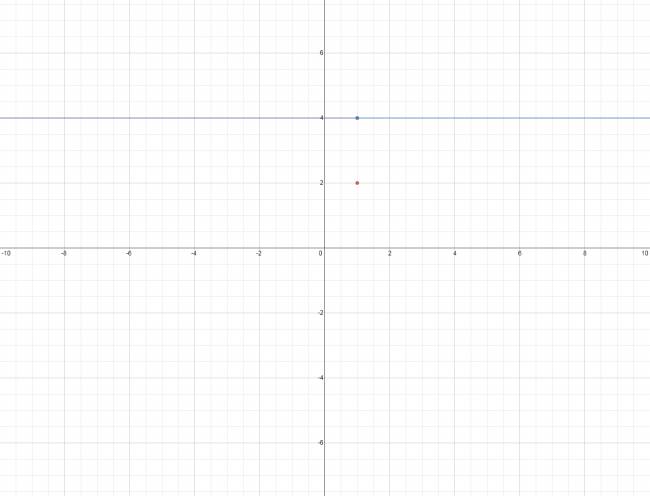
$$ f(x) = \begin{cases} 4 & \mbox{si } x>1 \\ 2 & \mbox{si } x=1 \\ 4 & \mbox{si } x<1 \end{cases} $$
Lo grafico:
Y por último, supongamos que se nos pide calcular el siguiente límite:
$$ \lim_{x \to 1} f(x) $$
¿El límite existe? ¿Cuánto da este límite?
Para calcular este límite, haremos hincapié en los límites laterales:
$$ \lim_{x \to 1^+} f(x) = 4 $$
$$ \lim_{x \to 1^-} f(x) = 4 $$
Y ahora podemos afirmar que:
$$ \lim_{x \to 1} f(x) = 4 $$
Ya te estás preguntando: ¿de qué me perdí? Pues, vamos a ver algunas cosas:
· La condición necesariamente y suficiente para que el límite de una función exista en un punto \( x=a \) es que existan sus límites laterales y que estos sean iguales.
· El límite de una función cuando tiende a \( x = a \) es el mismo al de sus límites laterales.
· Si no existen los límites laterales o estos son diferentes entre sí, no existirá el límite de la función en dicho punto.
Ejemplo:
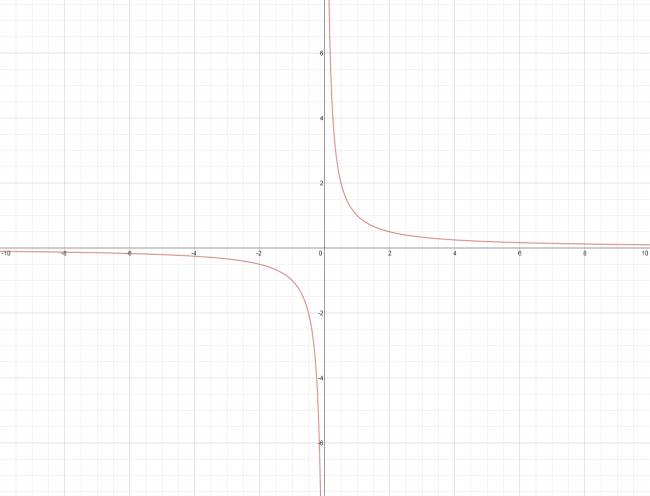
Supongamos la función: \( g(x) = \frac {1}{x} \), se nos pide calcular el siguiente límite:
$$ \lim_{x \to 0} g(x) $$
Lo grafico (para los que no conocen esta función):
Para activar las neuronas, vamos a calcular los límites laterales:
$$ \lim_{x \to 0^+} g(x) = +∞ $$
$$ \lim_{x \to 0^-} g(x) = -∞ $$
Como los límites laterales cuando \( x \to 0 \) son diferentes, afirmaré que el límite en dicho punto de abscisa no existe.
Ya hemos visto casos peculiares, ahora veamos casos más normales del cálculo de límites laterales.
Ejemplo:
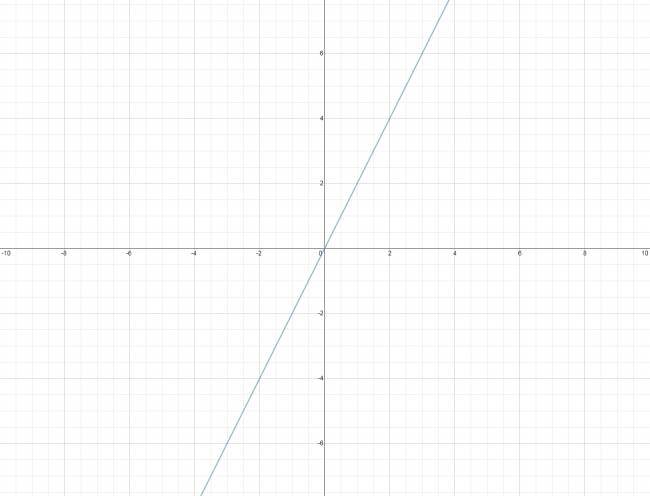
Sea la función \( h(x) = 2·x \), se pretende calcular los siguientes límites:
$$ \lim_{x \to 2^+} h(x) $$
$$ \lim_{x \to 2^-} h(x) $$
La grafico (para los despistados):
Como vemos, es una función continua, con poca gracia. Y veamos algo interesante:
$$ \lim_{x \to 2^+} h(x) = 4 $$
$$ \lim_{x \to 2^-} h(x) = 4 $$
En este caso, podemos afirmar lo siguiente:
$$ \lim_{x \to 2} h(x) = 4 $$
Acotaciones:
· Toda función polinómica es continua.
|
Infinitésimos:
Definición:
\( f \) es un infinitésimo \( ⇔ \lim_{x \to a} f(x) = 0 \).
El valor de tendencia puede ser un número cualquiera, inclusive cero y hasta infinito.
Propiedades:
· La suma de un número finito de infinitésimos es otro infinitésimo, para la misma tendencia en \( x \).
· El producto de un número finito de infinitésimos es también un infinitésimo, para la misma tendencia en \( x \).
· Si \( f \) es un infinitésimo cuando \( x \to a \) y \( h \) es una función acotada en un \( E^{*}_{(a, \delta)} \), entonces \( f·h \) es un infinitésimo cuando \( x \to a \).
Orden de los infinitésimos:
Sirve para comparar el orden de dos infinitésimos.
Basémonos en lo siguiente:
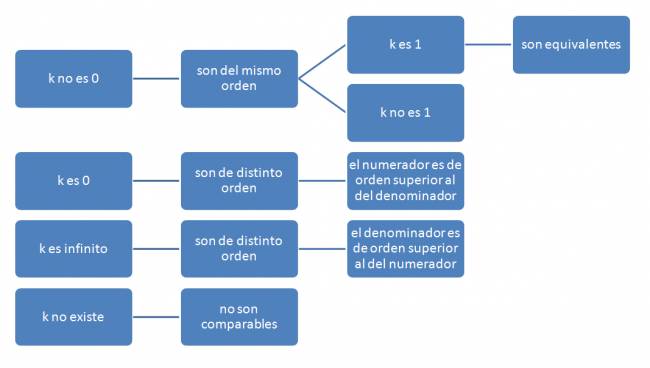
$$ \lim_{x \to a} f(x) = 0 ∧ \lim_{x \to a} g(x) = 0 ∧ g(x) ≠ 0 \mbox { en } E^{*}_{(a,\delta)} ⇒ \lim_{x \to a} \frac {f(x)}{g(x)} = k $$
Dependiendo de los valores de \( k \), podremos conocer su orden:
Infinitésimos equivalentes:
Definición:
Dos infinitésimos cuando \( x \to a \) son equivalentes si el límite del cociente de comparación es 1.
Expresado matemáticamente:
$$ \lim_{x \to a} \frac {f(x)}{g(x)} = 1 $$
|
Infinitos
No todas las funciones crecen de igual forma, hay algunas que lo hacen a "mayor velocidad" que otras.
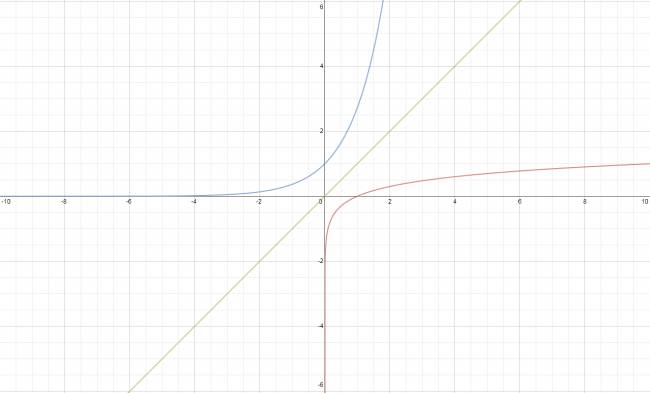
Veamos el siguiente gráfico:
$$ f(x) = e^{x} $$
$$ g(x) = x $$
$$ h(x) = \log x $$
· La función \( f(x) \) corresponde al de una función exponencial.
· La función \( g(x) \) corresponde al de una función potencial.
· La función \( h(x) \) corresponde al de una función logarítmica.
Como vemos, la que crece a "mayor velocidad" es la función exponencial, con esto me refiero que a menor abscisa alcanzará mayor ordenada con respecto a las otras funciones. Esto nos permite afirmar que la función exponencial es la que "llega más rápidamente" a infinito.
Órdenes:
Los órdenes nos permiten conocer qué tipos de funciones llegan más rápido a infinito:
Exponencial > Potencial > Logarítmica
Esto es muy último para cuando se dan indeterminaciones de cuando un límite tiende a infinito, nos podemos quedar con aquellos de mayor orden, y "olvidarnos" de aquellos con menor orden.
Acotaciones:
· Sólo se puede aplicar órdenes cuando se están realizando operaciones de multiplicación o división, en los casos de suma o resta esto no está permitido ya que no se cumple.
|