08-05-2013, 10:23 PM
Este es uno de esos temas que ya nos hacemos una idea por su título. Te puedo decir que una función es continua si cuando realizás el gráfico de una función, en ningún momento tenés que levantar el lápiz.
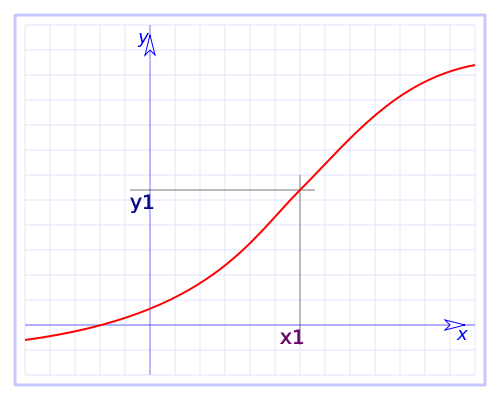
Definición de función continua en un punto:
La función \( f \) es continua en \( x = a \) y \(a∈Df ⇔ ∀ ε>0, ∃δ>0/x∈E_{(a,δ)} ⇒ f(x)∈ E_{(f(a),ε)} \).
Definición de función continua a partir de límite:
\( f \) es continua en \( x = a \) si y sólo si se cumplen las siguientes condiciones:
$$ \begin{cases} ∃f(a) \\ \\ ∃\lim_{x \to a} f(x) \\ \\ \lim_{x \to a} f(x) = f(a) \end{cases} $$

Definición de función continua en un punto:
La función \( f \) es continua en \( x = a \) y \(a∈Df ⇔ ∀ ε>0, ∃δ>0/x∈E_{(a,δ)} ⇒ f(x)∈ E_{(f(a),ε)} \).
Definición de función continua a partir de límite:
\( f \) es continua en \( x = a \) si y sólo si se cumplen las siguientes condiciones:
$$ \begin{cases} ∃f(a) \\ \\ ∃\lim_{x \to a} f(x) \\ \\ \lim_{x \to a} f(x) = f(a) \end{cases} $$