27-04-2013, 2:14 AM
· Función par:
Una función es par cuando: si se toma un número real \( x \), a la función le corresponde un valor \( a \), y cuando se considera al opuesto \( -x \), a la función le corresponde el mismo valor \( a \).
$$ f(x) = f(-x) $$
Esto es lo que sucede con las funciones cuadráticas del tipo: \( f(x) = x^2 \)
$$ (+1)^2 = (-1)^2 $$
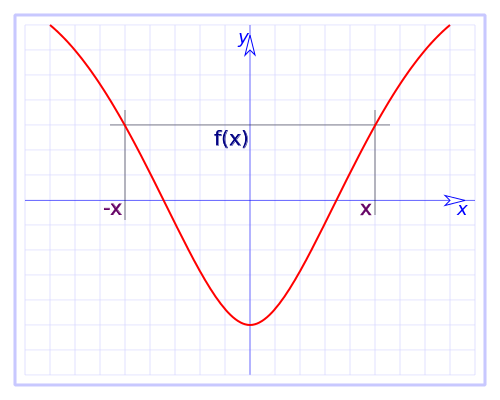
Este tipo de funciones tienen un eje de simetría respecto al eje de las ordenadas.
· Función impar:
Una función es impar cuando: si se toma un número real \( x \), a la función le corresponde un valor \( a \), y cuando se considera al opuesto \( -x \), a la función le corresponde el mismo valor \( -a \).
$$ f(x) = -f(-x) $$
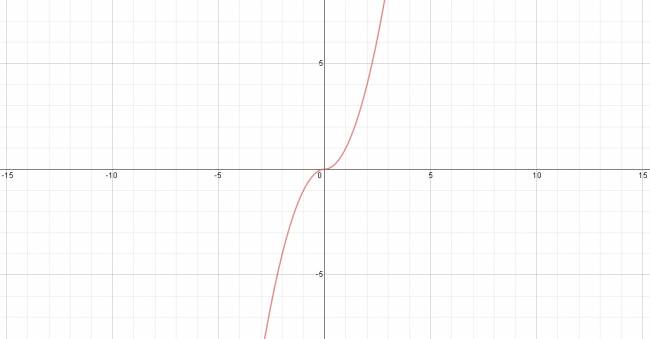
Esto es lo que sucede con las funciones cuadráticas del tipo: \( f(x) = x^3 \)
$$ (+1)^3 = - (-1)^3 $$

Este tipo de funciones tienen un eje de simetría respecto al origen.
Toda función polinómica es susceptible a esta clasificación. Si el grado de la función polinómica es par, esta función será par; por el contrario, si su grado es impar, la función será impar.
La función valor absoluto es un claro ejemplo de una función par.
Una función es par cuando: si se toma un número real \( x \), a la función le corresponde un valor \( a \), y cuando se considera al opuesto \( -x \), a la función le corresponde el mismo valor \( a \).
$$ f(x) = f(-x) $$
Esto es lo que sucede con las funciones cuadráticas del tipo: \( f(x) = x^2 \)
$$ (+1)^2 = (-1)^2 $$

Este tipo de funciones tienen un eje de simetría respecto al eje de las ordenadas.
· Función impar:
Una función es impar cuando: si se toma un número real \( x \), a la función le corresponde un valor \( a \), y cuando se considera al opuesto \( -x \), a la función le corresponde el mismo valor \( -a \).
$$ f(x) = -f(-x) $$
Esto es lo que sucede con las funciones cuadráticas del tipo: \( f(x) = x^3 \)
$$ (+1)^3 = - (-1)^3 $$

Este tipo de funciones tienen un eje de simetría respecto al origen.
Toda función polinómica es susceptible a esta clasificación. Si el grado de la función polinómica es par, esta función será par; por el contrario, si su grado es impar, la función será impar.
La función valor absoluto es un claro ejemplo de una función par.