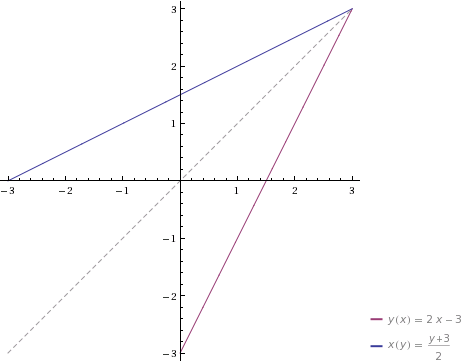26-04-2013, 3:41 AM
La inversa de una función \( f(x) \), es otra función \( f^{-1}(x) \) que tiene como dominio el recorrido de la función \( f(x) \) y como codominio el dominio de la función \( f(x) \). Para que una función tenga inversa es necesario que sea biyectiva.
A la función inversa de \( f(x) \) se la denota como \( f^{-1}(x) \).
Definición de función inversa:
$$ f(x) = y ⇔ f^{-1}(y) = x $$
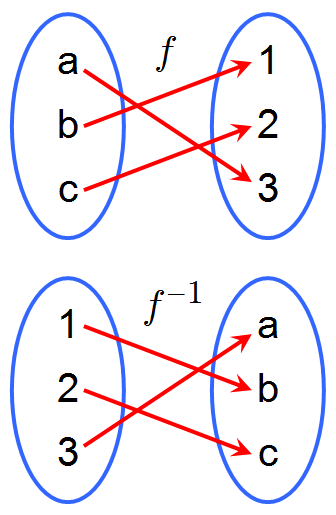
La mayoría de las funciones no tienen una función inversa asociada, algunas funciones que tienen inverso son:
· Función lineal o de primer grado.
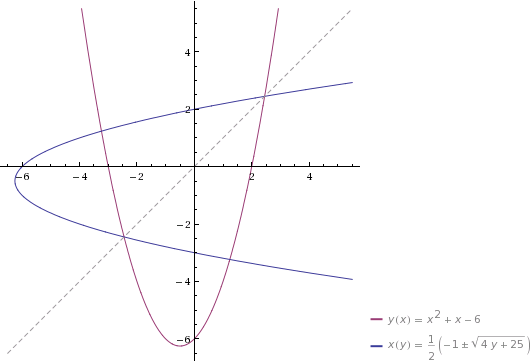
· Función cuadrática o de segundo grado.
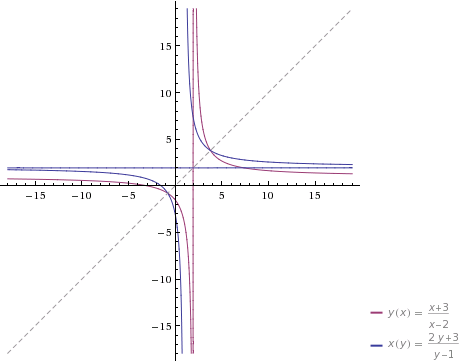
· Función racional.
Una función presenta un eje de simetría en \( x=y \) con respecto a su inversa. Tener en cuenta que: \( x=y \) es la bisectriz del primer y tercer cuadrante.
A la función inversa de \( f(x) \) se la denota como \( f^{-1}(x) \).
Definición de función inversa:
$$ f(x) = y ⇔ f^{-1}(y) = x $$

La mayoría de las funciones no tienen una función inversa asociada, algunas funciones que tienen inverso son:
· Función lineal o de primer grado.
· Función cuadrática o de segundo grado.
· Función racional.
Una función presenta un eje de simetría en \( x=y \) con respecto a su inversa. Tener en cuenta que: \( x=y \) es la bisectriz del primer y tercer cuadrante.
Cita
Tener muy en cuenta que:
$$ f^{-1}(x) ≠ \frac {1}{f(x)} $$
$$ f^{-1}(x) ≠ \frac {1}{f(x)} $$