25-04-2013, 3:27 AM
Pendiente de una recta
La pendiente de una recta o también conocido coeficiente angular, es lo que te dice cuán inclinada está una recta. Por ejemplo, en física, la pendiente de la gráfica x(t) nos da la velocidad.
La pendiente se puede definir como el incremento del eje vertical sobre el incremente del eje horizontal.
$$ p = \frac {\Delta y}{\Delta x} $$
Tener en cuenta que la letra griega mayúscula delta \( (\Delta) \) delante de una magnitud quiere decir variación de, por lo que la anterior expresión se puede escribir como:
$$ p = \frac {y_{f} - y_{i}}{x_{f} - x_{i}} $$
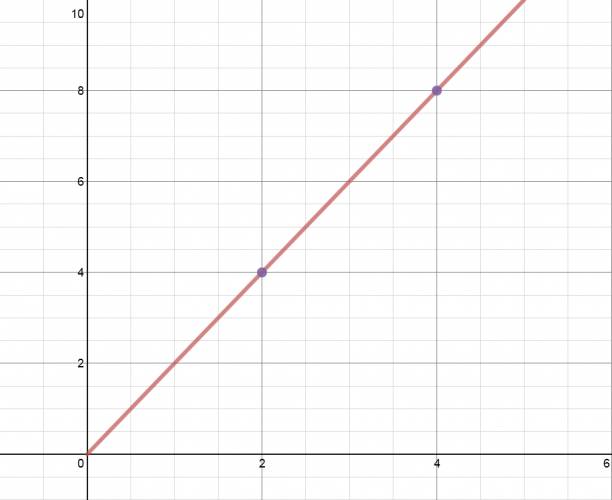
O sea, para calcular la pendiente de una recta, necesito sólo dos puntos distintos que pertenezcan a esta. Restamos los valores verticales y los dividimos entre la resta de los valores horizontales.
La pendiente de una recta o también conocido coeficiente angular, es lo que te dice cuán inclinada está una recta. Por ejemplo, en física, la pendiente de la gráfica x(t) nos da la velocidad.
La pendiente se puede definir como el incremento del eje vertical sobre el incremente del eje horizontal.
$$ p = \frac {\Delta y}{\Delta x} $$
Tener en cuenta que la letra griega mayúscula delta \( (\Delta) \) delante de una magnitud quiere decir variación de, por lo que la anterior expresión se puede escribir como:
$$ p = \frac {y_{f} - y_{i}}{x_{f} - x_{i}} $$
O sea, para calcular la pendiente de una recta, necesito sólo dos puntos distintos que pertenezcan a esta. Restamos los valores verticales y los dividimos entre la resta de los valores horizontales.