24-04-2013, 10:03 PM
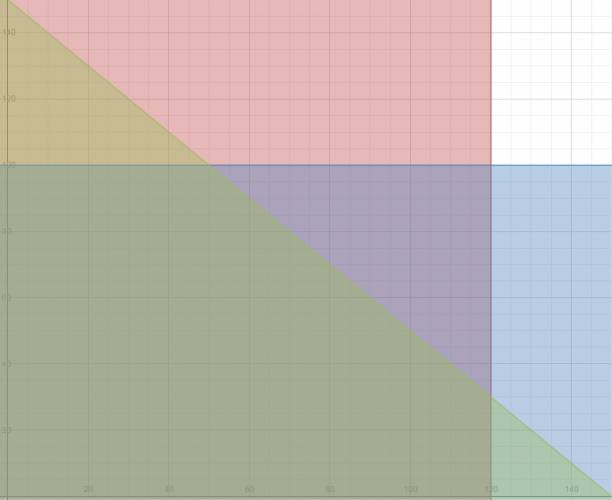
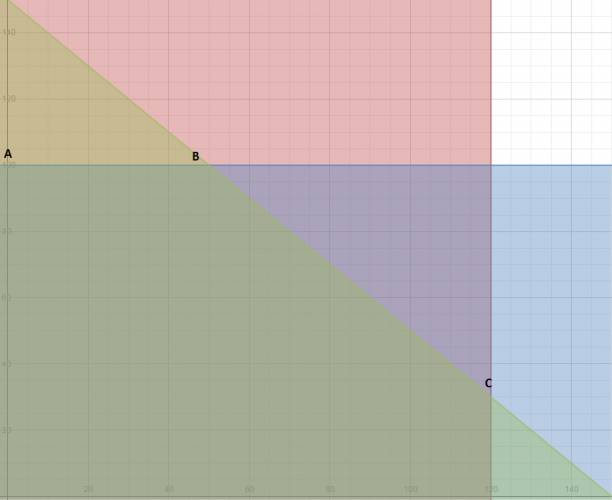
1. Un estudiante dedica parte de su tiempo al reparto de propaganda publicitaria. La empresa A le paga 5 pesos por cada impreso repartido y la empresa B, con folletos más grandes, le paga 7 pesos. por impreso. El estudiante lleva dos bolsas: una para los impresos A, en la que caben 120, y otra para los impresos B, en la que caben 100. Ha calculado que cada día es capaz de repartir 150 impresos como máximo. Lo que se pregunta el estudiante es: ¿cuántos impresos habrá que repartir de cada clase para que su beneficio diario sea máximo?
2. En una fábrica de bombillas se producen dos tipos de ellas, las de tipo normal valen 450 pesos y las halógenas 600 pesos. La producción está limitada por el hecho de que no pueden fabricarse al día más de 400 normales y 300 halógenas ni más de 500 en total. Si se vende toda la producción ¿cuántas de cada clase convendrá producir para obtener la máxima facturación?
3. En una avícola, se alimenta a los pollos con una dieta para engordar que tiene una composición mínima de 15 unidades de una sustancia A y 15 unidades de otra sustancia B. En el mercado sólo se encuentran dos tipos de raciones para aves: la ración X contiene 1 unidad de A y 5 unidades de B, la ración Y contiene 5 unidades de A y 1 unidad de B. ¿Qué cantidad de bolsas de cada tipo se deben comprar para cubrir las necesidades con un costo mínimo, y cuál es el costo?
4. Un agricultor comprará fertilizantes que contienen tres nutrientes: A, B y C. Los requerimientos mínimos semanales son 80 unidades de A, 120 de B y 240 de C. Existen dos mezclas populares de fertilizantes en el mercado. La mezcla I cuesta 4 dólares por bolsa, con 2 unidades de A, 6 de B y 4 de C. ¿Cuántas bolsas de cada mezcla debe comprar el agricultor para minimizar el costo de satisfacer sus requerimientos de nutrientes?
2. En una fábrica de bombillas se producen dos tipos de ellas, las de tipo normal valen 450 pesos y las halógenas 600 pesos. La producción está limitada por el hecho de que no pueden fabricarse al día más de 400 normales y 300 halógenas ni más de 500 en total. Si se vende toda la producción ¿cuántas de cada clase convendrá producir para obtener la máxima facturación?
3. En una avícola, se alimenta a los pollos con una dieta para engordar que tiene una composición mínima de 15 unidades de una sustancia A y 15 unidades de otra sustancia B. En el mercado sólo se encuentran dos tipos de raciones para aves: la ración X contiene 1 unidad de A y 5 unidades de B, la ración Y contiene 5 unidades de A y 1 unidad de B. ¿Qué cantidad de bolsas de cada tipo se deben comprar para cubrir las necesidades con un costo mínimo, y cuál es el costo?
4. Un agricultor comprará fertilizantes que contienen tres nutrientes: A, B y C. Los requerimientos mínimos semanales son 80 unidades de A, 120 de B y 240 de C. Existen dos mezclas populares de fertilizantes en el mercado. La mezcla I cuesta 4 dólares por bolsa, con 2 unidades de A, 6 de B y 4 de C. ¿Cuántas bolsas de cada mezcla debe comprar el agricultor para minimizar el costo de satisfacer sus requerimientos de nutrientes?