| Foro Problemas resueltos Circunferencias exteriores tangentes, demostrar rectas paral |
| Circunferencias exteriores tangentes, demostrar rectas paral |
07-10-2012, 5:56 PM
|
07-10-2012, 6:09 PM
Primero que nada haré un dibujo para tener una idea de lo que se habla en el ejercicio.
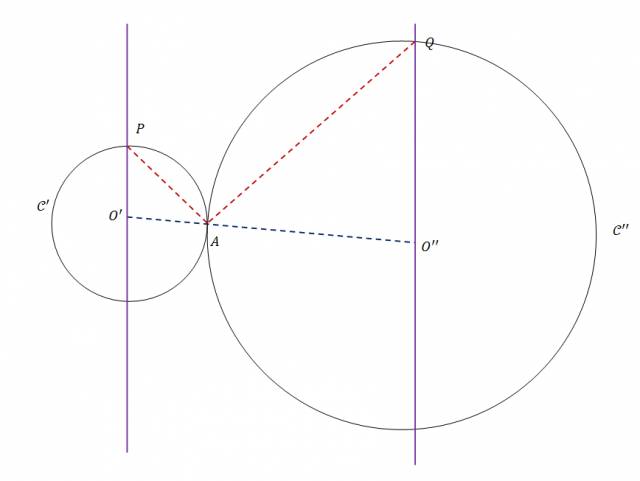
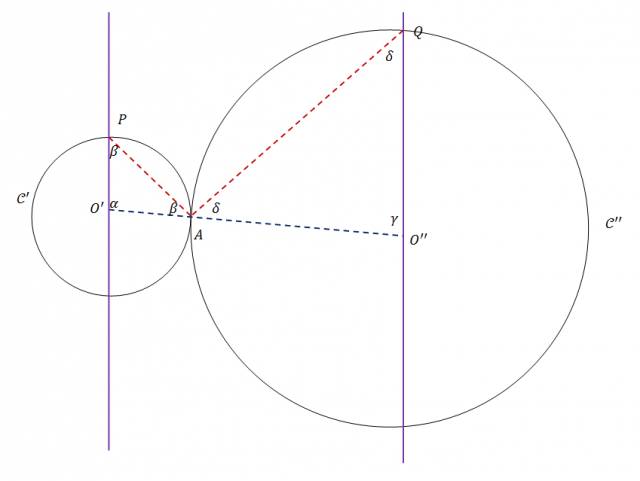
 Para entender mejor el razonamiento que voy a hacer, le voy a poner nombres a los ángulos.  Ahora estamos en condiciones de empezar a pensar el ejercicio. Quote Propiedad a tener en cuenta: La suma de todos los ángulos interiores de un triángulo siempre suman 180º. Sabemos que: α + β + β = 180º γ + δ + δ = 180º Deducimos que: α = 180º - 2·β γ = 180º - 2·δ Sumaré todo lo anterior: α = 180º - 2·β γ = 180º - 2·δ ------------------- α + γ = 360º - 2·(β + δ) Quote Propiedad a tener en cuenta: En dos circunferencias tangentes exteriores, los centros de las circunferencias como el punto de tangencia están alineados, o sea, están sobre una misma recta. Deducimos la figura que: β + δ = 90º α + γ = 360º - 2·(β + δ) α + γ = 360º - 2·(90º) α + γ = 360º - 180º α + γ = 180º ⇒ O'P || O''Q |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.