Universo Científico :: Problemas de tiro horizontal y velocidad media conoc gráfico

Página 1 de 1
1

Problemas de tiro horizontal y velocidad media conoc gráfico

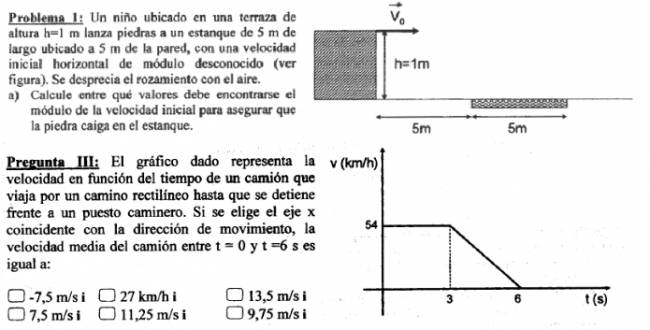
Problema 1:
Como se lanza horizontalmente podemos afirmar que la velocidad inicial en el eje y es nula:
$$ v_{oy} = 0 \frac {m}{s} $$

Lo que me piden es que calcule los valores de la velocidad en horizontal $ (v_{ox}) $ que hacen que el cuerpo caiga dentro de la estanque.

Antes que todo, tenemos que saber cuánto tiempo va a estar en el aire el cuerpo.
$$ \Delta y = v_{oy}·\Delta t + \frac {g·\Delta t^2}{2} $$
$$ 1,0 m = (0 \frac {m}{s})·\Delta t + \frac {10 \frac {m}{s^2}·\Delta t^2}{2} $$
$$ 1,0 m = \frac {10 \frac {m}{s^2}·\Delta t^2}{2} $$
$$ 1,0 m = 5,0 \frac {m}{s^2}·\Delta t^2 $$
$$ \Delta t = \sqrt {\frac {1,0 m}{5,0 \frac {m}{s^2}}} $$
$$ \Delta t = 0,45 s $$

Ahora, para saber qué velocidad necesita vamos a utilizar la fórmula de MRU ya que en el eje horizontal se mueve con este movimiento.
$$ v_{x} = \frac {\Delta x}{\Delta t} $$
El tiempo fue el que calculamos anteriormente y la distancia es el primer punto del estanque, o sea, a 5,0 m de donde se lanza la pelota. Sustituimos y llegamos a:
$$ v_{x} = \frac {5,0 m}{0,45 s} ⇒ v_{x} = 11 \frac {m}{s} $$

Y para calcular la velocidad "límite" vamos a tomar como 10 m la distancia, ya que tenemos desde que se lanza hasta el punto máximo que está a 10 m = 5,0 m + 5,0 m.
$$ v_{x} = \frac {10 m}{0,45 s} ⇒ v_{x} = 22 \frac {m}{s} $$

Podemos afirmar que:
$$ 11 \frac {m}{s} ≤ v_{x} ≤ 22 \frac {m}{s} $$

Pregunta III:
La forma más correcta de hacer este tipo de ejercicios es aplicando la definición de velocidad media, o sea, es el cociente entre el espacio recorrido entre la cantidad de tiempo empleado. Por esta razón vamos a proceder a calcular el desplazamiento total, para esto vamos a necesitar la gráfica.

Antes de hacer cualquier cosa, vemos que la velocidad están en km/h, por lo que vamos a proceder a pasarlo a m/s; para esto simplemente vamos a dividir el 54 entre 3,6 lo que nos da: 15

Ahora sí vamos a trabajar bien con la gráfica: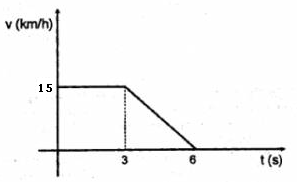

Recordemos que el área de la gráfica $ v(t) $ nos da el desplazamiento del móvil, y eso es justamente lo que vamos a calcular.
Podemos calcular el área total como la suma del área del rectángulo y el área del triángulo, pero yo lo voy a calcular como el área del trapecio.
$$ \Delta x = \frac {(6+3)·15}{2} ⇒ \Delta x = 67,5 m $$

Ahora, como vimos en el gráfico, el móvil se desplazó durante 6,0 s. Ahora vamos aplicar la fórmula de velocidad media:
$$ v_{x} = \frac {\Delta x}{\Delta t} ⇒ v_{x} = \frac {67,5 m}{6,0 s} ⇒ v_{x} = 11,25 \frac {m}{s} $$

Página 1 de 1
1

Universo Científico

marcos364

Admin

Admin