Características generales:
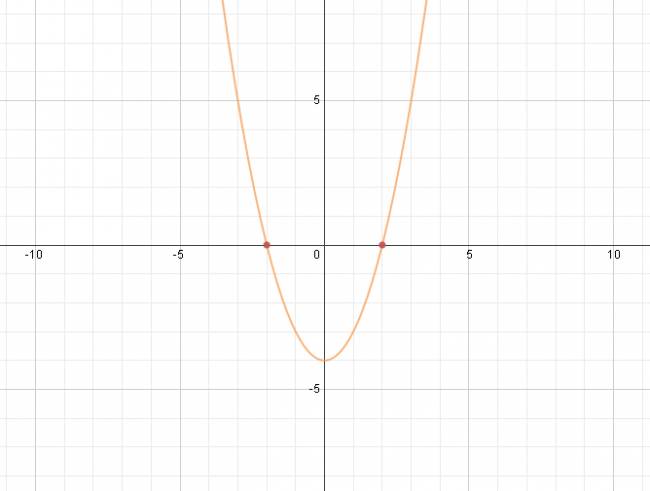
· Raíces:
Las raíces de una función, son los puntos del plano resultantes de la intersección del gráfico con el eje x. Tener en cuenta que no siempre una función cuadrática corta el eje x. Las raíces se pueden calcular igualando el polinomio a cero. Por ejemplo: sea la función \( f(x) = 2·x^2 + 3·x + 4 \), sus raíces se pueden calcular como: \( 2·x^2 + 3·x + 4 = 0 \). Para saber cómo se resuelve la anterior ecuación, ver: ecuación cuadrática o de segundo grado.
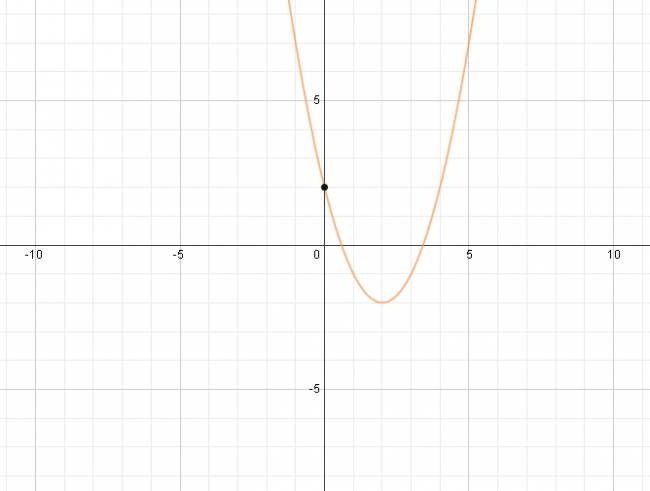
· Ordenada en el origen:
La ordenada en el origen de una función, es el punto del plano resultante de la intersección del gráfico con el eje y. Toda ecuación cuadrática tiene una única ordenada en el origen. La ordenada en el origen se puede conocer por simple inspección del polinomio, ya que el término independiente coincide con esta.
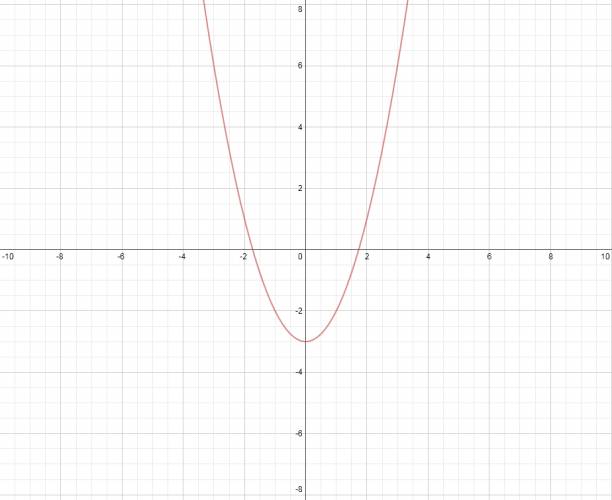
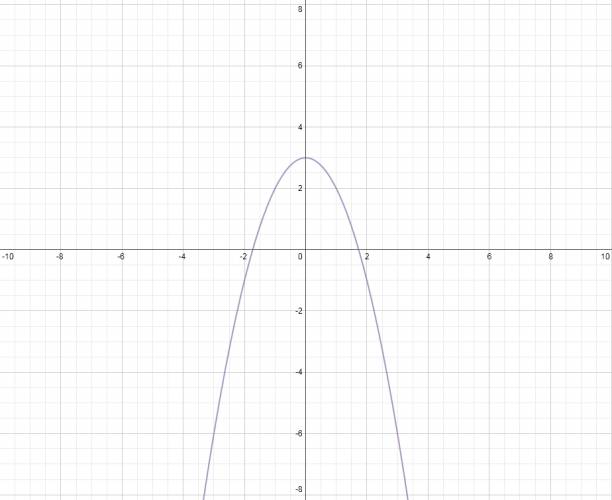
· Concavidad:
Si el coeficiente del término principal es un número positivo, la parábola tendrá concavidad positiva, mientras que si es un número negativo, la parábola tendrá concavidad negativa.
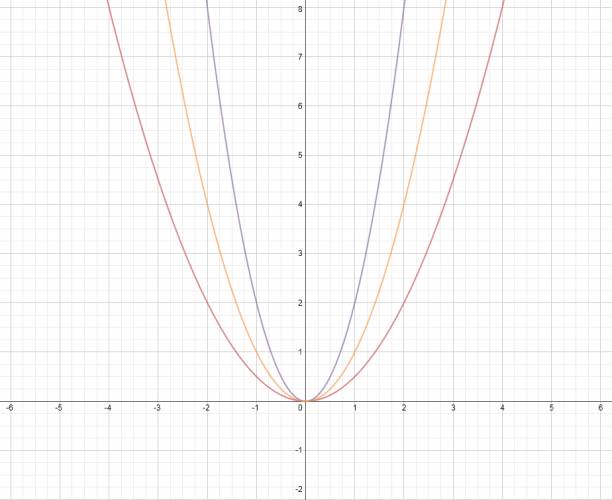
· Apertura:
La apertura de la parábola es lo que me permite saber cuan abierta o cuan cerrada está.
Cuanto mayor sea el valor absoluto del coeficiente del término principal, más cerrada estará la parábola.
Cuanto menor sea el valor absoluto del coeficiente del término principal, más abierta estará la parábola.
· Vértice:
El vértice de la parábola es un punto: es el máximo de esta, si tiene concavidad negativa, mientras que es el mínimo si tiene concavidad positiva.
$$ v (v_{x}, v_{y}) $$