24-01-2013, 5:44 PM
Sea la función:
$$ f(x) = \frac {3·x - 6}{6·x + 12} ≥ 0 $$
Estudiar:
· Raíces
· Asíntotas
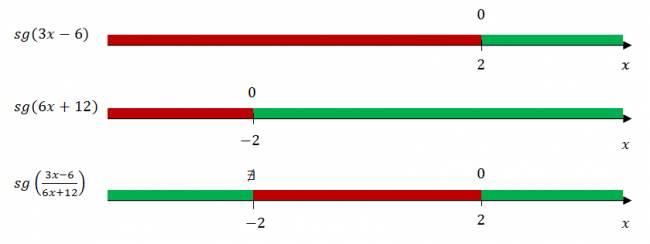
· Estudio del signo
· Conjunto solución
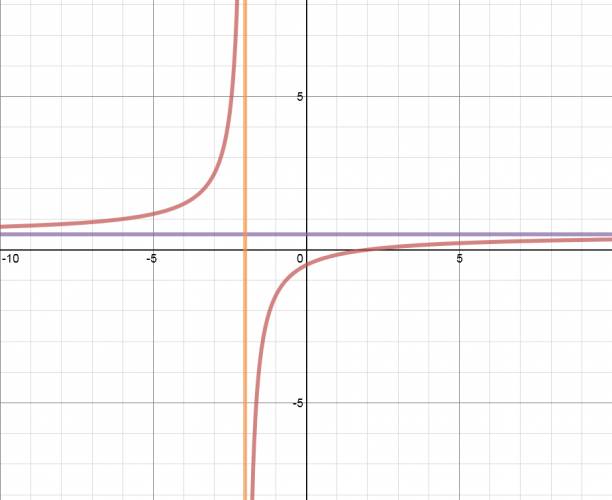
· Graficarla
$$ f(x) = \frac {3·x - 6}{6·x + 12} ≥ 0 $$
Estudiar:
· Raíces
· Asíntotas
· Estudio del signo
· Conjunto solución
· Graficarla