23-01-2013, 10:22 PM
Esquema de división de Ruffini para divisores de primer grado
El esquema de división de Paolo Ruffini, es un método muy rápido para hallar el cociente y el resto resultantes de dividir un polinomio de segundo grado en adelante, entre otro de primer grado.
Se hace una tabla en la que se trabajará con los coeficientes del los polinomios.
En la primer fila, a partir de la segunda columna, se anotarán los coeficientes de polinomio a dividir (polinomio dividendo), ocupando, los coeficientes cada uno una columna.
En la segunda fila, primera columna, se anotará la raíz del polinomio a dividir (polinomio divisor).
En la tercera fila, a partir de la segunda columna, se escribirán los coeficientes del polinomio cociente, mientras que el último lugar de esta fila será ocupado por el resto.
Siempre que falte un coeficiente, se podrá 0.

Esquema de división de Ruffini para divisores de forma la \( (x-α) \)
Sea \( f(x) \) un polinomio de grado \( n \), con \( n > 1 \); de la forma: \( f(x) = a_{n}·x^{n} + a_{n-1}·x^{n-1} + ... + a_{1}·x + a_{0} \).
Sea \( z(x) \) un polinomio de primer grado, de la forma \( (x-α) \).
Se pretende hallar el cociente \( q(x) \) y resto \( r(x) \) de la división de \( f(x) \) entre \( z(x) \).
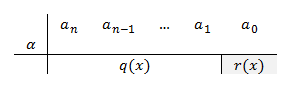
Esquema de división de Ruffini para divisores de forma la \( (a·x+b) \)
Sea \( f(x) \) un polinomio de grado \( n \), con \( n > 1 \); de la forma: \( f(x) = a_{n}·x^{n} + a_{n-1}·x^{n-1} + ... + a_{1}·x + a_{0} \).
Sea \( z(x) \) un polinomio de primer grado, de la forma \( (a·x+b) \).
Se pretende hallar el cociente \( q(x) \) y resto \( r(x) \) de la división de \( f(x) \) entre \( z(x) \).
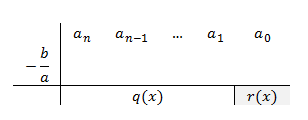
El esquema de división de Paolo Ruffini, es un método muy rápido para hallar el cociente y el resto resultantes de dividir un polinomio de segundo grado en adelante, entre otro de primer grado.
Se hace una tabla en la que se trabajará con los coeficientes del los polinomios.
En la primer fila, a partir de la segunda columna, se anotarán los coeficientes de polinomio a dividir (polinomio dividendo), ocupando, los coeficientes cada uno una columna.
En la segunda fila, primera columna, se anotará la raíz del polinomio a dividir (polinomio divisor).
En la tercera fila, a partir de la segunda columna, se escribirán los coeficientes del polinomio cociente, mientras que el último lugar de esta fila será ocupado por el resto.
Siempre que falte un coeficiente, se podrá 0.

Esquema de división de Ruffini para divisores de forma la \( (x-α) \)
Sea \( f(x) \) un polinomio de grado \( n \), con \( n > 1 \); de la forma: \( f(x) = a_{n}·x^{n} + a_{n-1}·x^{n-1} + ... + a_{1}·x + a_{0} \).
Sea \( z(x) \) un polinomio de primer grado, de la forma \( (x-α) \).
Se pretende hallar el cociente \( q(x) \) y resto \( r(x) \) de la división de \( f(x) \) entre \( z(x) \).
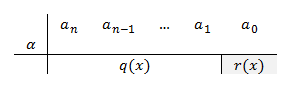
Esquema de división de Ruffini para divisores de forma la \( (a·x+b) \)
Sea \( f(x) \) un polinomio de grado \( n \), con \( n > 1 \); de la forma: \( f(x) = a_{n}·x^{n} + a_{n-1}·x^{n-1} + ... + a_{1}·x + a_{0} \).
Sea \( z(x) \) un polinomio de primer grado, de la forma \( (a·x+b) \).
Se pretende hallar el cociente \( q(x) \) y resto \( r(x) \) de la división de \( f(x) \) entre \( z(x) \).
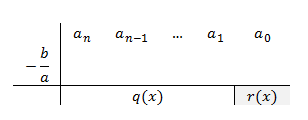
Quote
Recordemos que la raíz de un binomio de primer grado de la forma \( (a·x+b) \) es \( x = - \frac {b}{a} \).
Quote
Atención: (otra regla más)
Para dividir una función polinómica \( p(x) \) entre un divisor de la forma \( (a·x+b) \), usando el método de Ruffini, se divide \( p(x) \) entre \( (x-α) \), siendo \( α = - \frac {b}{a} \).
1. Al cociente \( q'(x) \) de esta división auxiliar, habrá que dividirlo entre \( α \), para obtener el cociente buscado, es decir: \( q(x) = \frac {q'(x)}{a} \).
2. El resto de esta división es el mismo que el resto buscado.
Para dividir una función polinómica \( p(x) \) entre un divisor de la forma \( (a·x+b) \), usando el método de Ruffini, se divide \( p(x) \) entre \( (x-α) \), siendo \( α = - \frac {b}{a} \).
1. Al cociente \( q'(x) \) de esta división auxiliar, habrá que dividirlo entre \( α \), para obtener el cociente buscado, es decir: \( q(x) = \frac {q'(x)}{a} \).
2. El resto de esta división es el mismo que el resto buscado.