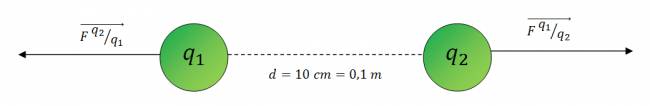01-12-2012, 7:36 PM
- Página 1 de 1
- 1
| Foro Problemas resueltos Refracción, ley de Snell, ondas, ley de Coulomb, electrostát |
| Refracción, ley de Snell, ondas, ley de Coulomb, electrostát |
| |
01-12-2012, 7:40 PM
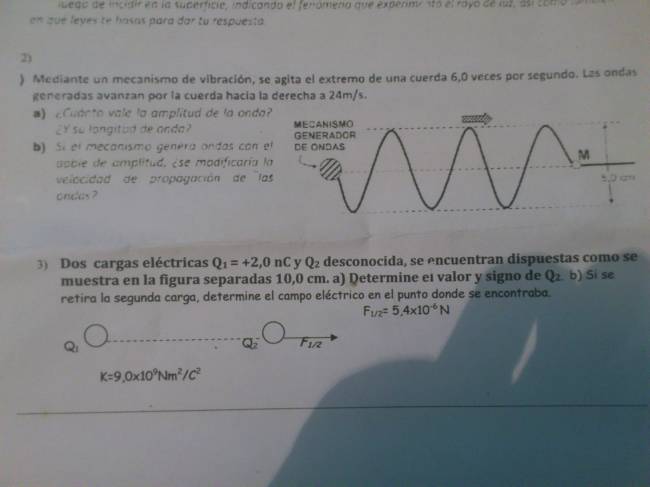
Primer ejercicio:
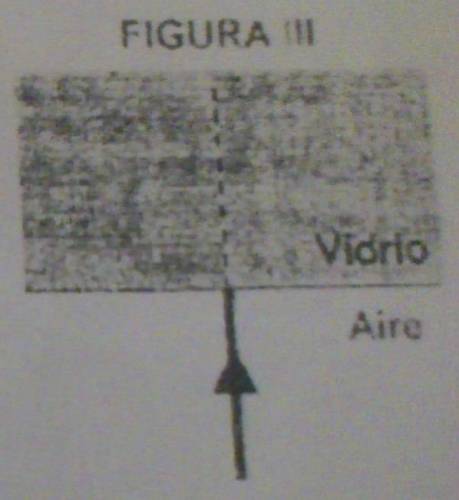
FIGURA I:  El ángulo marcado en la imagen es del rayo con respecto a el medio, pero para aplicar la ley de Snell debemos tomar el ángulo formado por el rayo con respecto a la normal (es la línea punteada que aparece en la imagen). Si realizamos las cuentas veremos que el ángulo es de 60º con respecto a la normal.  Conocemos los índices de refracción de ambos medios: \( n_{aire} = 1,00 \) \( n_{vidrio} = 1,41 \) Quote Recordar que los índices de refracción son adimensionados (no poseen unidades). Finalmente aplicamos la ley de Snell: $$ n_{1}· sen \alpha_{1} = n_{2}· sen \alpha_{2} $$ Tomaré los siguientes medios:  $$ 1,00· sen 60º = 1,41· sen \alpha_{2} $$ Despejamos: $$ \frac {1,00· sen 60º}{1,41} = sen \alpha_{2} $$ $$ sen \alpha_{2} = \frac {1,00· 0,866}{1,41} = 0,614 $$ Lo que hicimos fue hallar el seno del ángulo, para hallar el ángulo debemos realizar la operación opuesta al seno, la cual es el arcoseno o sen[sup]-1[sup], en la calcularado se hace utilizando la función SHIFT + sin. $$ arcosen (0,614) = 37,9 º$$ Finalmente, el ángulo es de 37,9º; ahora lo representamos en la figura:  |
02-12-2012, 4:45 PM
FIGURA II:
 Hacemos lo mismo que con la anterior, marcamos el ángulo de incidencia y los medios:  Y ahora planteamos la ley de Snell: $$ n_{1}· sen \alpha_{1} = n_{2}· sen \alpha_{2} $$ $$ 1,41· sen 60º = 1,00· sen \alpha_{2} $$ $$ sen \alpha_{2} = \frac {1,41· sen 60º}{1,00} $$ $$ sen \alpha_{2} = \frac {1,41· 0,866}{1,00} $$ $$ sen \alpha_{2} = 1,22 $$ Si hacemos la inversa de seno para conocer el ángulo nos encontraremos con un error matemático, el seno de cualquier ángulo es menor o igual a 1. Por esta razón se dice que hay una reflexión interna total. Se representa de la siguiente manera:  |
02-12-2012, 4:58 PM
FIGURA II:
 Nuevamente, marcamos los medios y el ángulo de incidencia:  El ángulo de incidencia es 0º y está sobre la normal. Aplicamos la ley de Snell: $$ n_{1}· sen \alpha_{1} = n_{2}· sen \alpha_{2} $$ $$ 1,00· sen 0º = 1,41· sen \alpha_{2} $$ $$ sen \alpha_{2} = \frac {1,00· sen 0º}{1,41} $$ $$ sen \alpha_{2} = \frac {1,00· 0}{1,41} $$ $$ sen \alpha_{2} = 0 $$ $$ \alpha_{2} = 0º $$ Ahora lo representamos:  |
02-12-2012, 5:08 PM
|
02-12-2012, 5:12 PM
Segundo problema:
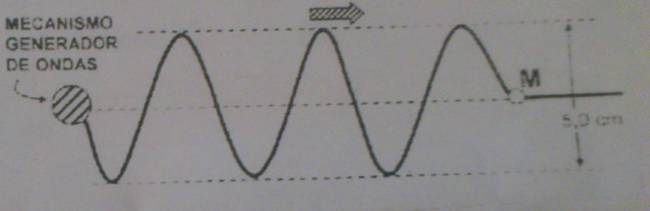 Quote El problema habla de que la cuerda se agita 6 veces por segundo, lo que significa que está hablando de frecuencia. Por lo tanto, la frecuencia de la onda es de 6 Hz. Sacamos los datos del problema: \( v_{p} = 24 \frac {m}{s} \) \( f = 6,0 Hz \) Hallaré la longitud de onda (\( \lambda \)): $$ v_{p} = \lambda · f \Rightarrow \lambda = \frac {v_{p}}{f} \Rightarrow \lambda = 4,0 m$$ La amplitud la sacás del dibujo: 2,5 cm = 0,025 m Parte b: No, la amplitud no está en ninguna fórmula, por lo que no tiene relación directa con las demás características cuantificables de la onda. |
02-12-2012, 5:25 PM
Tercer problema:
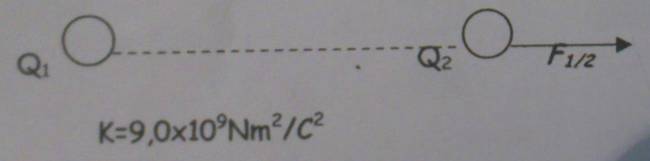 Aplicamos la ley de Coulomb y la despejamos para obtener el valor de la segunda carga: $$ F = \frac{k·q_{1}·q_{2}}{d^2} \Rightarrow q_{2} = \frac {F · d^2}{k·q_{1}}$$ Ahora sustituimos en la fórmula despejada para conocer el valor de la segunda carga: $$ q_{2} = \frac {(5,4·10^{-6} N) · (0,1 m)^2}{(9·10^9 \frac{N·m^2}{C^2})·(2,0·10^{-9} C)}$$ $$ q_{2} = 3,0 · 10^{-9} C = 3,0 nC$$ Quote Tener en cuenta que: 10 cm = 0,1 m Quote nC significa nanoculombio, lo que hace es multiplica por \(10^{-9}\). Sabemos que la carga \(q_{1}\) es positiva (letra del problema), y sabemos que la carga \(q_{2}\) está apuntando hacia el lado opuesto de la primer carga, esto quiere decir que tienen la misma carga (ambos son protones). Y así será la representación:  |
02-12-2012, 5:50 PM
|
- Página 1 de 1
- 1