29-11-2012, 7:41 PM
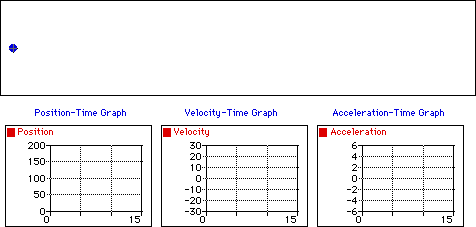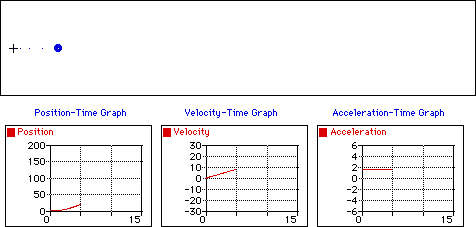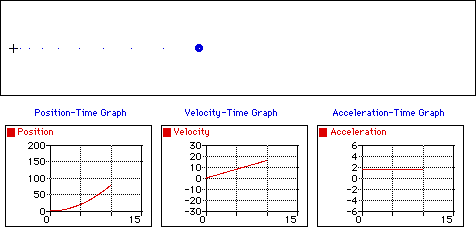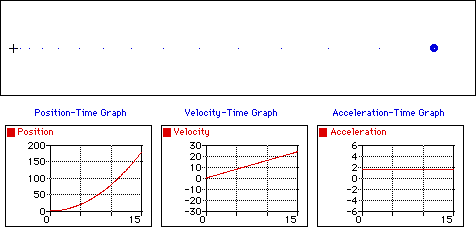
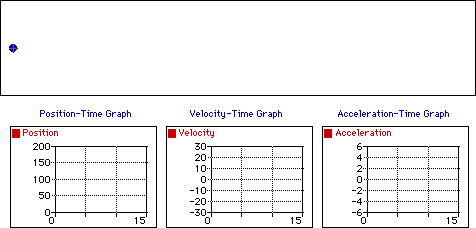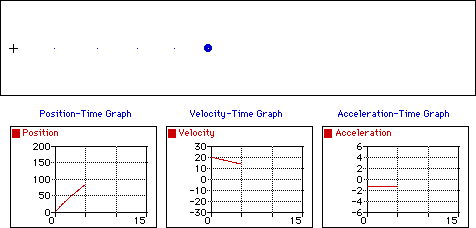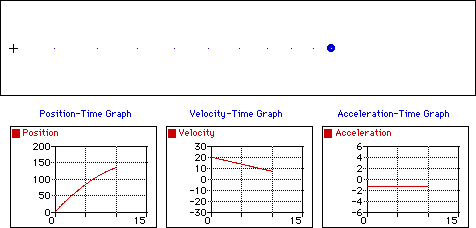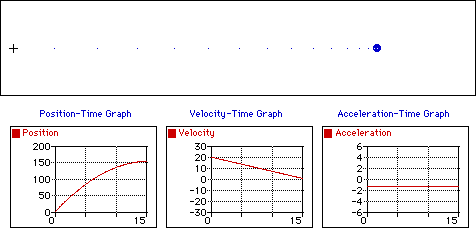
M.R.U.V. (Movimiento Rectilíneo Uniformemente Variado)
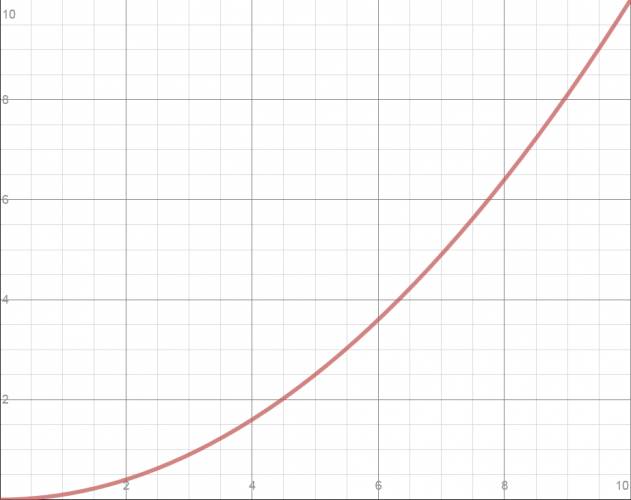
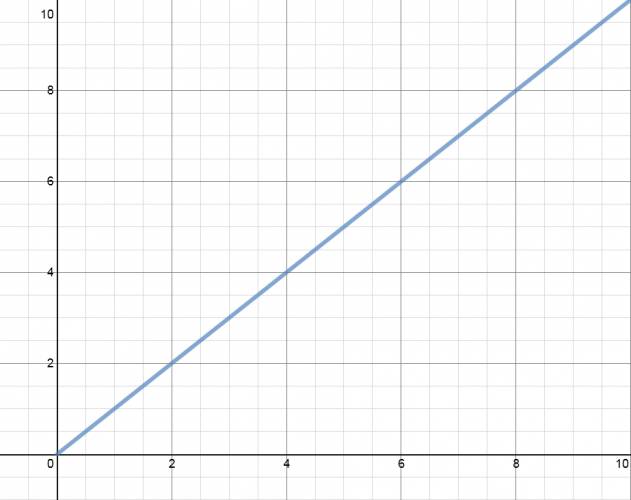
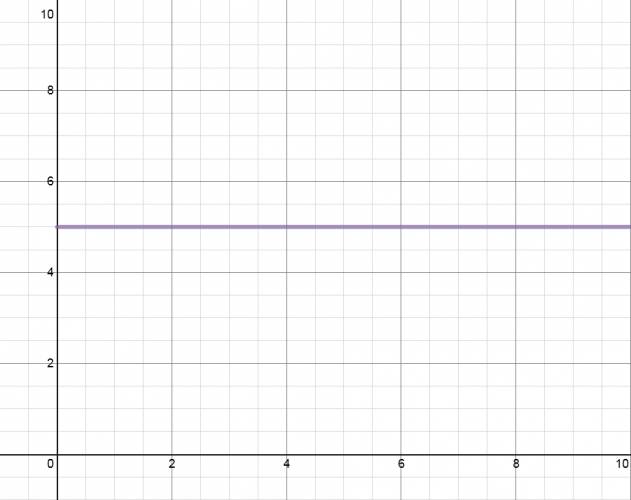
También se conoce como M.R.U.A. (Movimiento Rectilíneo Uniformemente Acelerado), esto se de a que actúa la aceleración (\(a≠0\)). Este movimiento se caracteriza por tener aceleración constante: \(a=cte\).
Definición de aceleración:
La aceleración es la variación que presenta la velocidad en la unidad de tiempo.
Fórmulas:
También se conoce como M.R.U.A. (Movimiento Rectilíneo Uniformemente Acelerado), esto se de a que actúa la aceleración (\(a≠0\)). Este movimiento se caracteriza por tener aceleración constante: \(a=cte\).
Definición de aceleración:
La aceleración es la variación que presenta la velocidad en la unidad de tiempo.
Fórmulas:
Cita
$$ a= \frac{ \Delta v}{ \Delta t} $$
$$ v_{f} = v_{o} + a· \Delta t $$
$$ x_{f} = x_{i} + v_{o}· \Delta t + \frac {a· \Delta t^2}{2} $$
$$ \Delta x = \frac{v_{f}^2 - v_{i}^2}{2·a} $$
$$ \Delta x = \frac{(v_{f} + v_{i})· \Delta t}{2} $$

$$ v_{f} = v_{o} + a· \Delta t $$
$$ x_{f} = x_{i} + v_{o}· \Delta t + \frac {a· \Delta t^2}{2} $$
$$ \Delta x = \frac{v_{f}^2 - v_{i}^2}{2·a} $$
$$ \Delta x = \frac{(v_{f} + v_{i})· \Delta t}{2} $$