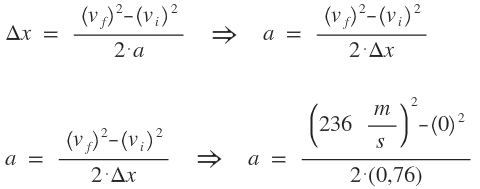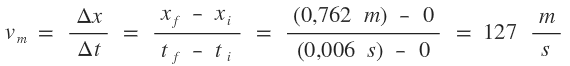| Foro Problemas resueltos Problema de movimiento variado, bala de cañón |
| Problema de movimiento variado, bala de cañón |
21-09-2012, 7:25 PM
|
21-09-2012, 7:47 PM
Cómo el ejercicio habla desde que la bala es disparada hasta que pasa por la boca del cañón, puedo afirmar que:
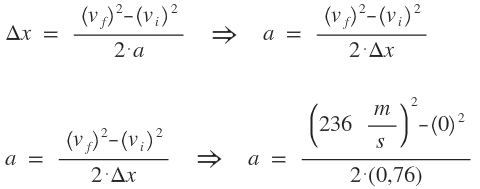
vo = 0 (parte del reposo) vf = 850 km/h = 236 m/s ∆x = 30 pulgadas = 76,2 cm = 0,76 m Comenzaré desde abajo con las preguntas: · Primero hallaré la aceleración: Los datos que conozco con: desplazamiento total, velocidad inicial, velocidad final, por lo que utilizaré la siguiente fórmula:  a = 36.642 m/s2 · Hallaré el tiempo necesario: ∆x = vo·∆t + 1/2·a·∆t2 0,76 m = (0)·∆t + 1/2·(36.642 m/s2)·∆t2 0,76 m = 1/2·(36.642 m/s2)·∆t2 2·(0,76 m) = (36.642 m/s2)·∆t2 1,52 m = (36.642 m/s2)·∆t2 (1,52 m)/(36.642 m/s2) = ∆t2 ∆t = √((1,52 m)/(36.642 m/s2)) ∆t = 0,006 s · Hallaré la velocidad media:  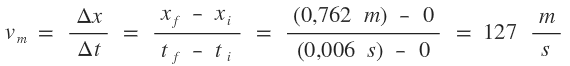vm = 127 m/s Quote Respuestas: a. La velocidad media de la bala mientras se acelera dentro del cañón es de 127 m/s (357,2 km/h). b. El tiempo empleado en recorrer la longitud del cañón es de 0,006 s. c. La aceleración de la basa es de 36.642 m/s2. |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.