12-11-2012, 6:07 PM
Número complejo
Un número complejo es la unión del conjunto de los números reales y el conjunto de los números imaginarios: \( ℝ ∪ \Im = ℂ \).
Definición:
Los números complejos son de la forma binómica \( a + b·i \), donde \( a \) es la parte real, \( b \) es la parte imaginaria e \( i \) es la unidad imaginaria pura.
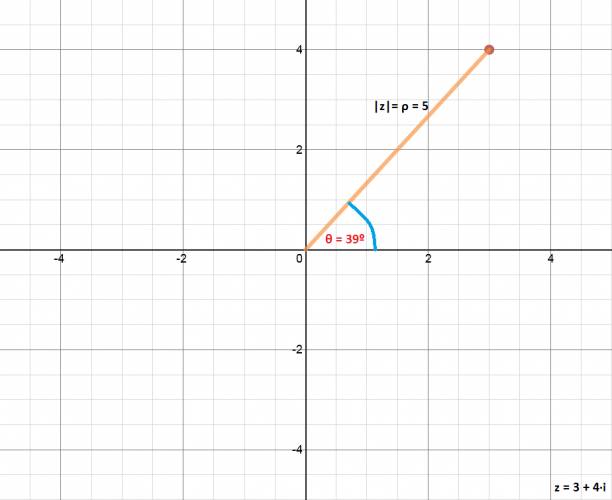
A los números complejos se los puede representar en un plano de ejes cartesiano (diagrama de Argand), lo cual se conoce como notación cartesiana. La parte real es la abscisa mientras que la parte imaginaria es la ordenada:
Notaciones:
· Notación binómica:
\( z = a + b·i \)
· Notación cartesiana:
\( z (a, b) \)
· Notación trigonométrica:
\( z = r·(cos \theta + i·sen \theta) \)
· Notación polar:
\( z = \rho ∠ \theta \)
Siendo:
· \( \rho = |z| \) (módulo)
· \( \theta = \) ángulo (argumento)
Pudiéndose calcular como:
· \( |z| = \sqrt {a^2 + b^2} \)
· \( \theta = \arctan \left ( \frac {b}{a} \right ) \)
Regla de conversión:
\( a = |z|·cos \theta \)
\( b = |z|·sen \theta \)
Tener en cuenta que:
Para el caso en que \( a = 0 \), el afijo pertenece al eje \( y ⇒ \theta = \frac {\pi}{2} = 90º ∨ \theta = \frac {3·\pi}{2} =270º \).
Igualdad de números complejos:
Dos números complejos \( z = a + b·i \) y \( w = c + d·i \) son iguales si tienen la misma parte real y la misma parte imaginaria:
$$ a + b·i = c + d·i ⇔ a = c ∧ b = d $$
Conjugado de un número complejo:
Sea \( z = a + b·i \) un número complejo, su conjugado será \( \overline z = a - b·i \). O sea, el conjugado de un número complejo, es otro número complejo que tiene igual parte real y opuesta parte imaginaria.
Propiedad de la suma: la suma de dos números complejos conjugados siempre da otro número complejo real puro (sin parte imaginaria) y del doble de la parte real:
$$ z + \overline z = (a + b·i) + (a - b·i) = 2·a $$
Propiedad del producto: el producto de dos números complejos conjugados siempre da otro número complejo real puro (sin parte imaginaria):
$$ z · \overline z = (a + b·i) · (a - b·i) = a^2 + b^2 $$
Más propiedades delos complejos conjugados:
1. \( \overline z + \overline w = \overline {(z + w)} \)
2. \( \overline z · \overline w = \overline {(z · w)} \)
3. \( \frac {\overline z}{\overline w} = \overline { \frac {z}{w} } \)
4. \( k· \overline z = \overline {k·z}, k∊ℝ \)
5. \( (\overline z)^n = \overline {z^n}, n∊ℕ \)
Un número complejo es la unión del conjunto de los números reales y el conjunto de los números imaginarios: \( ℝ ∪ \Im = ℂ \).
Definición:
Los números complejos son de la forma binómica \( a + b·i \), donde \( a \) es la parte real, \( b \) es la parte imaginaria e \( i \) es la unidad imaginaria pura.
A los números complejos se los puede representar en un plano de ejes cartesiano (diagrama de Argand), lo cual se conoce como notación cartesiana. La parte real es la abscisa mientras que la parte imaginaria es la ordenada:
Notaciones:
· Notación binómica:
\( z = a + b·i \)
· Notación cartesiana:
\( z (a, b) \)
· Notación trigonométrica:
\( z = r·(cos \theta + i·sen \theta) \)
· Notación polar:
\( z = \rho ∠ \theta \)
Siendo:
· \( \rho = |z| \) (módulo)
· \( \theta = \) ángulo (argumento)
Pudiéndose calcular como:
· \( |z| = \sqrt {a^2 + b^2} \)
· \( \theta = \arctan \left ( \frac {b}{a} \right ) \)
Regla de conversión:
\( a = |z|·cos \theta \)
\( b = |z|·sen \theta \)
Tener en cuenta que:
Para el caso en que \( a = 0 \), el afijo pertenece al eje \( y ⇒ \theta = \frac {\pi}{2} = 90º ∨ \theta = \frac {3·\pi}{2} =270º \).
Igualdad de números complejos:
Dos números complejos \( z = a + b·i \) y \( w = c + d·i \) son iguales si tienen la misma parte real y la misma parte imaginaria:
$$ a + b·i = c + d·i ⇔ a = c ∧ b = d $$
Conjugado de un número complejo:
Sea \( z = a + b·i \) un número complejo, su conjugado será \( \overline z = a - b·i \). O sea, el conjugado de un número complejo, es otro número complejo que tiene igual parte real y opuesta parte imaginaria.
Propiedad de la suma: la suma de dos números complejos conjugados siempre da otro número complejo real puro (sin parte imaginaria) y del doble de la parte real:
$$ z + \overline z = (a + b·i) + (a - b·i) = 2·a $$
Propiedad del producto: el producto de dos números complejos conjugados siempre da otro número complejo real puro (sin parte imaginaria):
$$ z · \overline z = (a + b·i) · (a - b·i) = a^2 + b^2 $$
Más propiedades delos complejos conjugados:
1. \( \overline z + \overline w = \overline {(z + w)} \)
2. \( \overline z · \overline w = \overline {(z · w)} \)
3. \( \frac {\overline z}{\overline w} = \overline { \frac {z}{w} } \)
4. \( k· \overline z = \overline {k·z}, k∊ℝ \)
5. \( (\overline z)^n = \overline {z^n}, n∊ℕ \)
