   |
| Foro » Departamento de Matemática » Teóricos » Graficar: funciones, ecuaciones, inecuaciones, ... |
| Graficar: funciones, ecuaciones, inecuaciones, ... |
|
19-11-2013, 8:07 AM
Post: #11
|
|||
|
|||
|
Parábola
Dada la ecuación de una parábola se nos pide graficarla. Salvo situaciones extrañas (que no voy a estudiar en este momento), se nos pueden presentar sólo dos tipos de ecuaciones de parábolas: \( y = a·x^2 + b·x + c \) o \( x = a·y^2 + b·y + c \). No existe ningún instrumento para dibujar una parábola, por lo que tendremos que basarnos en cosas más teóricas. Propiedad: Cuando mayor sea \( |a| \), más abierta será la parábola; cuánto menor sea, más cerrada será. 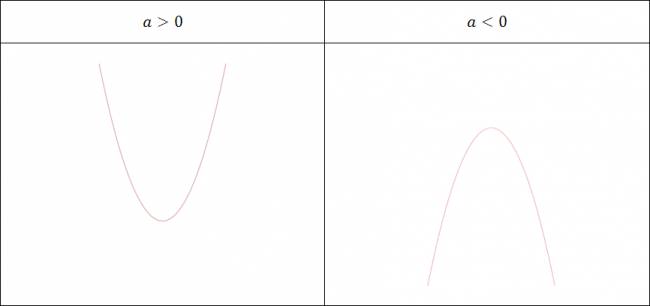Primer caso: Parábola de ecuación: \( y = a·x^2 + b·x + c \) Las parábolas de este tipo de ecuación serán de dos forman, dependiendo exclusivamente del signo de \( a \).  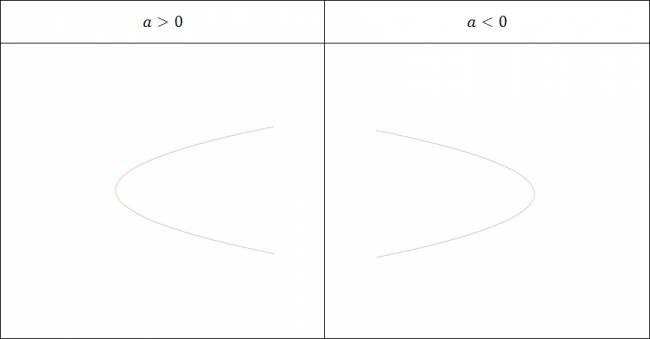Para hallar el vértice: $$ V (\frac {-b}{2·a}, \frac {4·a·c-b^2+1}{4·a}) $$ Segundo caso: Parábola de ecuación: \( x = a·y^2 + b·y + c \) Las parábolas de este tipo de ecuación serán de dos forman, dependiendo exclusivamente del signo de \( a \).  Para hallar el vértice: $$ V (\frac {4·a·c-b^2+1}{4·a}, \frac {-b}{2·a}) $$ En todos los casos, nos ayudaremos a graficarla hallando sus raíces y su ordenada en el origen. Todo esto lo debemos hacer considerando con respecto a cuál variable estamos trabajando. A lo que me refiero es que siempre se debe trabajar con el polinomio, la variable que se encuentre sola en un miembro de la igualdad, deberá ser reemplazada por cero para estudiar las raíces y la ordenada en el origen. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
  |
|
23-11-2013, 6:32 AM
Post: #12
|
|||
|
|||
|
Elipse
Para graficar una elipse (a mano alzada) necesitamos únicamente los cuatro vértices de ésta. Se intentará hacer el mejor "redondel" que pase simultáneamente por los cuatro. Aquí cuando vamos entrando con el tema cónicas se nos presentarán varios problemas. Estos problemas son que: si se te dan la ecuación de la elipse en forma reducida, genial; pero la mayoría de las veces se nos da la ecuación desarrollada y tendremos que reducirla y llevarla a la forma de una elipse reducida, y acá la cosa se complica, sobretodo porque es necesario aplicar conceptos de las llamadas matemáticas superiores como es el caso de derivadas parciales; y sí, un tema de cálculo se puede mezclar con uno de geometría analítica (lo verás más seguido de lo que crees). Supongamos que se nos da la ecuación de una elipse desarrollada, será de la forma: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \) Ahora bien, lo que nos interesa de la anterior expresión es hallar sus 4 vértices, pero, ¿cómo logramos esta odisea? Hallar vértices de una elipse conociendo su ecuación desarrollada: Lo que se pretenderá, será llegar a una expresión como la siguiente, donde sabemos que \( a \) y \( b \) son los vértices: $$ \frac {(x-h)^2}{a^2} + \frac {(y-k)^2}{b^2} = 1 $$ 1. Se debe hallar el centro de la elipse, esto lo haremos a través de derivadas parciales. Aprender cómo. 2. Ahora que conocemos el centro, podemos desarrollar los cuadrados de binomio (numeradores de ambas fracciones). $$ (x-h)^2 = x^2 - 2·x·h + h^2 $$ $$ (y-k)^2 = y^2 - 2·y·k + k^2 $$ 3. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |