26-10-2012, 9:57 PM
Es un teorema matemático que permite calcular un tercer lado de un triángulo cualquiera, conociendo su ángulo y los otros dos lados. En algunos países también se conoce como ley de los cosenos.
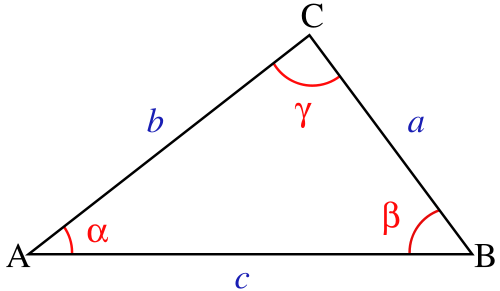
Enunciado del teorema:
En todo triángulo se cumple que el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos por el opuesto del doble de los otros dos lados por el coseno del ángulo del lado que se desea hallar.
Expresión matemática del teorema:
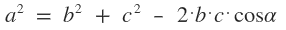
Despejado para hallar el ángulo:
$$ \hat A = \arccos (\frac {-a^2 + b^2 + c^2}{2·b·c}) $$
Demostración: http://www.x.edu.uy/teocose.swf
Generalización del teorema del coseno para hallar la diagonal más larga del un paralelogramo:
La diagonal más corta de cualquier paralelogramo se puede hallar con el teorema del coseno (fórmula que está más arriba).
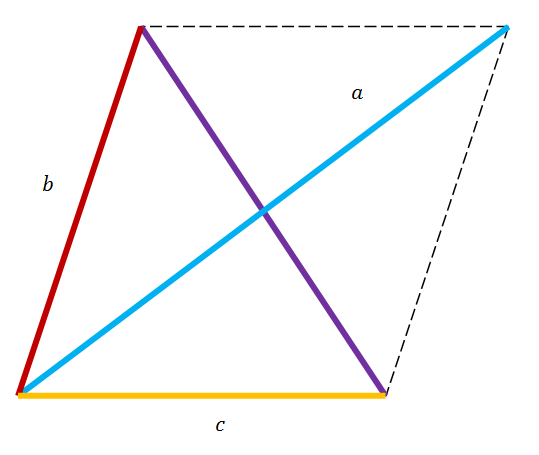
Como se muestra en el anterior caso, la diagonal más larga de un paralelogramo agudo, se puede hallar de la siguiente manera:
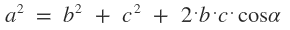
Ver ejemplo

Enunciado del teorema:
En todo triángulo se cumple que el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos por el opuesto del doble de los otros dos lados por el coseno del ángulo del lado que se desea hallar.
Expresión matemática del teorema:
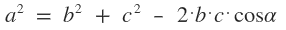
Despejado para hallar el ángulo:
$$ \hat A = \arccos (\frac {-a^2 + b^2 + c^2}{2·b·c}) $$
Demostración: http://www.x.edu.uy/teocose.swf
Generalización del teorema del coseno para hallar la diagonal más larga del un paralelogramo:
La diagonal más corta de cualquier paralelogramo se puede hallar con el teorema del coseno (fórmula que está más arriba).

Como se muestra en el anterior caso, la diagonal más larga de un paralelogramo agudo, se puede hallar de la siguiente manera:
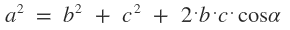
Ver ejemplo