15-11-2013, 1:32 AM
Función polinómica
Una función polinómica, es aquella función que tiene la forma:
$$ f(x) = \sum_{i=0}^{i=n} (a_{i}·x^{i}) $$
Las funciones polinómicas se diferencian dependiendo su grado. El grado es el mayor exponente al que está elevada la variable si su coeficiente no es nulo. Recordemos que los coeficientes siempre deben ser número reales.
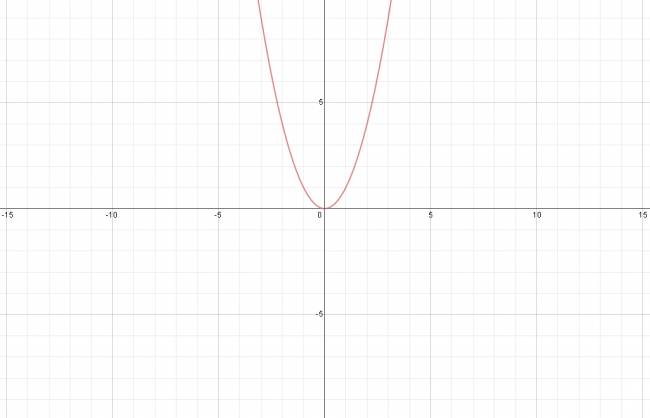
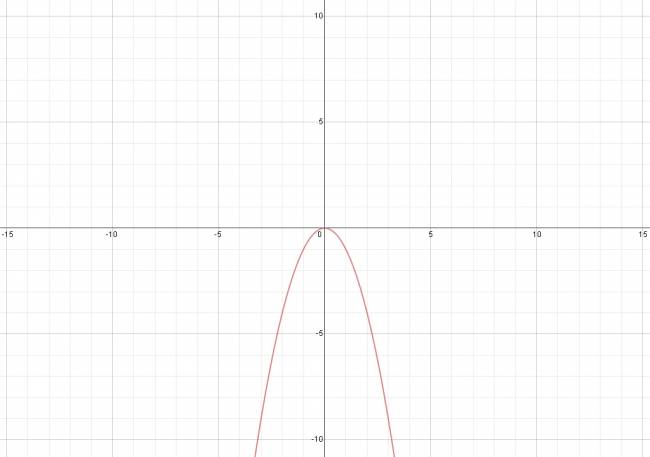
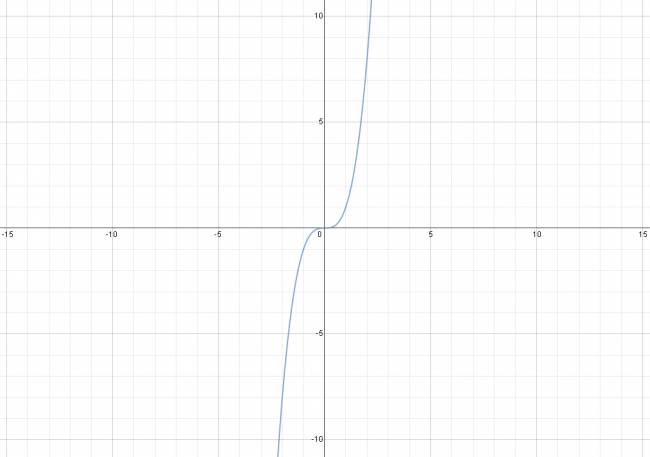
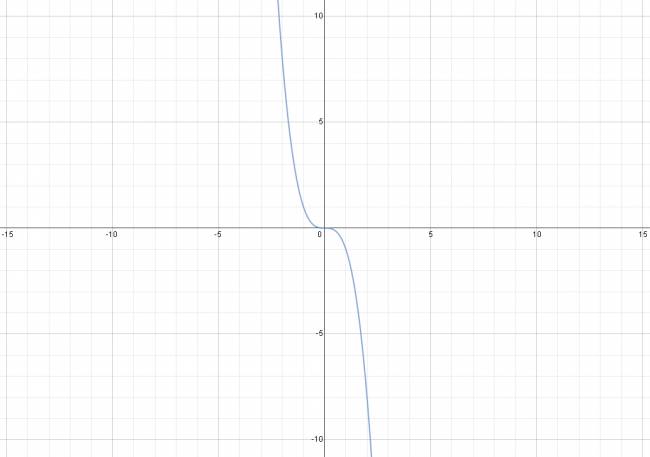
Las funciones de primer y segundo grado son las más conocidas y estudiadas, pues su representación gráfica siempre es la misma. Las funciones polinómicas de grado tercero en adelante, difieren entre sí, dependiendo de sus coeficientes.
El dominio de todas las funciones polinómicas es el conjunto de los números reales. Con el codominio la cosa varía. El codominio de las funciones de grado impar, es el conjunto de los números reales.
Propiedades importantes:
· Las funciones de grado segundo en adelante, presentan dirección asintótica paralela al eje \( O \vec y \).
· Todas las funciones polinómicas son continuas.
· Las funciones polinómicas no presentan puntos singulares.
· Toda función polinómica de grado impar, tiene al menos una raíz real.
Teoremas:
· Teorema de descomposición factorial: toda función polinómica, se puede expresar como factores, de la forma:
$$ f(x) = a·(x-\alpha_{1})·(x-\alpha_{2})·...·(x-\alpha_{n}) $$ donde \( a \) es el coeficiente del término principal, y \( \alpha \) son las raíces del polinomio.
· Teorema del resto: el resto de dividir una función polinómica \( p(x) \) entre un binomio \( (x - a) \), es igual a \( p(a) \).· Teorema de Descartes: la condición necesaria y suficiente para que \( p(x) \) sea divisible entre \( (x-a) \) es que \( a \) sea raíz de \( p(x) \).
Una función polinómica, es aquella función que tiene la forma:
$$ f(x) = \sum_{i=0}^{i=n} (a_{i}·x^{i}) $$
Las funciones polinómicas se diferencian dependiendo su grado. El grado es el mayor exponente al que está elevada la variable si su coeficiente no es nulo. Recordemos que los coeficientes siempre deben ser número reales.
Las funciones de primer y segundo grado son las más conocidas y estudiadas, pues su representación gráfica siempre es la misma. Las funciones polinómicas de grado tercero en adelante, difieren entre sí, dependiendo de sus coeficientes.
El dominio de todas las funciones polinómicas es el conjunto de los números reales. Con el codominio la cosa varía. El codominio de las funciones de grado impar, es el conjunto de los números reales.
Propiedades importantes:
· Las funciones de grado segundo en adelante, presentan dirección asintótica paralela al eje \( O \vec y \).
· Todas las funciones polinómicas son continuas.
· Las funciones polinómicas no presentan puntos singulares.
· Toda función polinómica de grado impar, tiene al menos una raíz real.
Teoremas:
· Teorema de descomposición factorial: toda función polinómica, se puede expresar como factores, de la forma:
$$ f(x) = a·(x-\alpha_{1})·(x-\alpha_{2})·...·(x-\alpha_{n}) $$ donde \( a \) es el coeficiente del término principal, y \( \alpha \) son las raíces del polinomio.
· Teorema del resto: el resto de dividir una función polinómica \( p(x) \) entre un binomio \( (x - a) \), es igual a \( p(a) \).
Demostración:
Hipótesis:
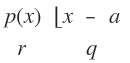
Tesis:
\( p(a) = r \)
Demostración:
por definición de división: \( p(x) = (x-a)·q + r \)
$$ p(a) = (a-a)·q + r \Rightarrow p(a) = 0 + r \Rightarrow p(a) = r ∎ $$
Hipótesis:
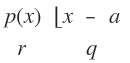
Tesis:
\( p(a) = r \)
Demostración:
por definición de división: \( p(x) = (x-a)·q + r \)
$$ p(a) = (a-a)·q + r \Rightarrow p(a) = 0 + r \Rightarrow p(a) = r ∎ $$
Demostración:
Definición de raíz de un polinomio:
\( a \) es raíz de \( p(x) ⇔ p(a) = 0 \)
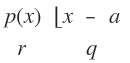
Por definición de división:
$$ p(x) = (x-a)·q + r $$
Si efectuamos: \( x = a \)
$$ p(a) = (a-a)·q + r $$
Por definición de raíz de un polinomio tenemos que: \( p(a) = 0 \)
$$ 0 = (a-a)·q + r $$
$$ 0 = 0·q + r $$
$$ 0 = r $$
Por definición, una división exacta es aquella en la que el resto es 0.
\( ∴ p(x) \) es divisible entre \( (x-a) ⇔ a \) es raíz de \( p(x) ∎ \)
Definición de raíz de un polinomio:
\( a \) es raíz de \( p(x) ⇔ p(a) = 0 \)
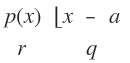
Por definición de división:
$$ p(x) = (x-a)·q + r $$
Si efectuamos: \( x = a \)
$$ p(a) = (a-a)·q + r $$
Por definición de raíz de un polinomio tenemos que: \( p(a) = 0 \)
$$ 0 = (a-a)·q + r $$
$$ 0 = 0·q + r $$
$$ 0 = r $$
Por definición, una división exacta es aquella en la que el resto es 0.
\( ∴ p(x) \) es divisible entre \( (x-a) ⇔ a \) es raíz de \( p(x) ∎ \)