05-11-2013, 5:25 PM
Integrales
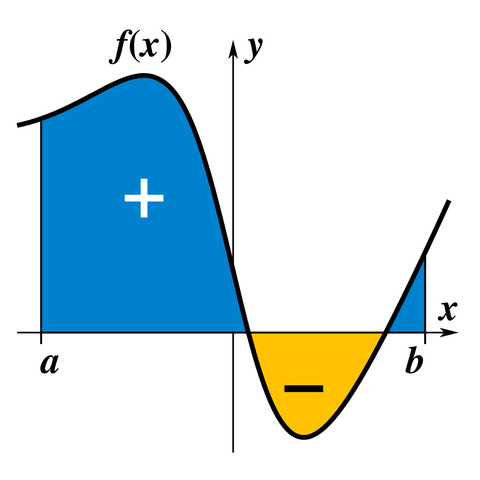
Comúnmente se conoce que las integrales permiten calcular el área debajo de curvas.
Primitiva (también conocida como antiderivada):
Sea una función \( f(x) \), afirmaremos que la primitiva es: \( F(x) \) y cumple que \( F'(x) = f(x) \).
Otra notación:
$$ \int f(x) \, dx $$
Léase: "integral de \( f \) de \( x \), diferencial \( x \)".
¿Por qué es necesario el \( dx \) al final? Es necesario ya que en cursos posteriores, donde se integren funciones compuestas por más variables, de debe saber respecto a qué variable se está derivando o integrando. El \( dx \) nos dice -en este caso- que estamos integrando para la variable \( x \).
Integral indefinida:
$$ \int f(x) \, dx = F(x) + c, c∈ℝ $$
Integral definida:
Sea \( f \) una función y un intervalo [a,b]:
$$ \int_{a}^{b} f(x) \, dx $$
Regla de Barrow:
Esta regla nos permite calcular el área debajo de un intervalo cerrado perteneciente al dominio de la función, de la siguiente manera:
$$ \int_{a}^{b} f(x) \, dx = F(b) - F(a) $$
Comúnmente se conoce que las integrales permiten calcular el área debajo de curvas.

Primitiva (también conocida como antiderivada):
Sea una función \( f(x) \), afirmaremos que la primitiva es: \( F(x) \) y cumple que \( F'(x) = f(x) \).
Otra notación:
$$ \int f(x) \, dx $$
Léase: "integral de \( f \) de \( x \), diferencial \( x \)".
¿Por qué es necesario el \( dx \) al final? Es necesario ya que en cursos posteriores, donde se integren funciones compuestas por más variables, de debe saber respecto a qué variable se está derivando o integrando. El \( dx \) nos dice -en este caso- que estamos integrando para la variable \( x \).
Integral indefinida:
$$ \int f(x) \, dx = F(x) + c, c∈ℝ $$
Integral definida:
Sea \( f \) una función y un intervalo [a,b]:
$$ \int_{a}^{b} f(x) \, dx $$
Regla de Barrow:
Esta regla nos permite calcular el área debajo de un intervalo cerrado perteneciente al dominio de la función, de la siguiente manera:
$$ \int_{a}^{b} f(x) \, dx = F(b) - F(a) $$