11-10-2013, 6:38 PM
Hipérbola equilátera
Una hipérbola es equilátera si y sólo si sus dos asíntotas son perpendiculares entre sí. Lo cual corresponde a que \( a = b \).
Expresión general:
$$ x·y = k $$
Condición:
\( k∈ℝ^{*} \)
Este tipo de hipérbola presenta dos tipos de gráficos distintos dependiendo del valor del número real no nulo \( k \).
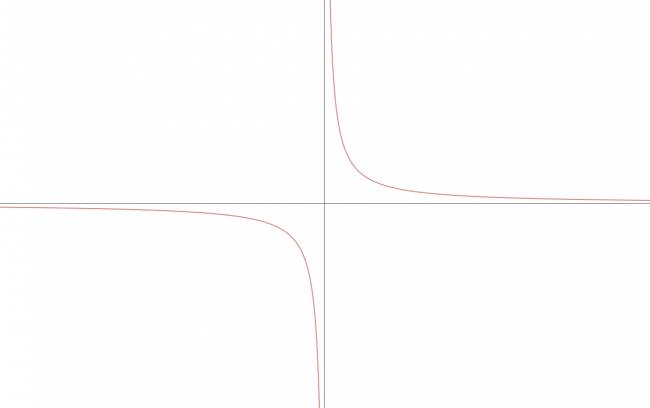
Si \( k > 0 \):
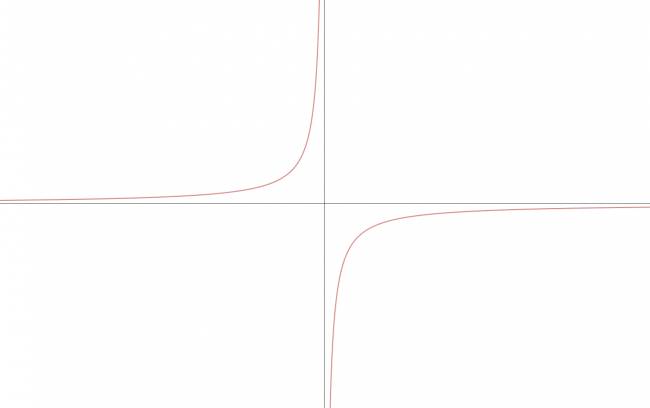
Si \( k < 0 \):
Una hipérbola es equilátera si y sólo si sus dos asíntotas son perpendiculares entre sí. Lo cual corresponde a que \( a = b \).
Expresión general:
$$ x·y = k $$
Condición:
\( k∈ℝ^{*} \)
Este tipo de hipérbola presenta dos tipos de gráficos distintos dependiendo del valor del número real no nulo \( k \).
Si \( k > 0 \):
Cita
Elementos:
· Focos: \( F (a,a) \) y \( F'(-a,-a) \)
· Asíntotas:
$$ ( r ) x = 0 $$
$$ ( s ) y = 0 $$
· Vértices:
$$ A (\frac {a}{\sqrt{2}},\frac {a}{\sqrt{2}}) $$
$$ A' (-\frac {a}{\sqrt{2}},-\frac {a}{\sqrt{2}}) $$
Relación importante:
$$ k = \frac {a^2}{2} $$
· Focos: \( F (a,a) \) y \( F'(-a,-a) \)
· Asíntotas:
$$ ( r ) x = 0 $$
$$ ( s ) y = 0 $$
· Vértices:
$$ A (\frac {a}{\sqrt{2}},\frac {a}{\sqrt{2}}) $$
$$ A' (-\frac {a}{\sqrt{2}},-\frac {a}{\sqrt{2}}) $$
Relación importante:
$$ k = \frac {a^2}{2} $$
Si \( k < 0 \):
Cita
Elementos:
· Focos: \( F (-a,a) \) y \( F'(a,-a) \)
· Asíntotas:
$$ ( r ) x = 0 $$
$$ ( s ) y = 0 $$
· Vértices:
$$ A (-\frac {a}{\sqrt{2}},\frac {a}{\sqrt{2}}) $$
$$ A' (\frac {a}{\sqrt{2}},-\frac {a}{\sqrt{2}}) $$
Relación importante:
$$ k = -\frac {a^2}{2} $$
· Focos: \( F (-a,a) \) y \( F'(a,-a) \)
· Asíntotas:
$$ ( r ) x = 0 $$
$$ ( s ) y = 0 $$
· Vértices:
$$ A (-\frac {a}{\sqrt{2}},\frac {a}{\sqrt{2}}) $$
$$ A' (\frac {a}{\sqrt{2}},-\frac {a}{\sqrt{2}}) $$
Relación importante:
$$ k = -\frac {a^2}{2} $$