23-10-2012, 6:19 PM
La geometría analítica es la rama de la matemática encargada del estudio de las figuras geométricas representadas en planos de ejes, más precisamente a la relación existente entre las ecuaciones y las figuras geométricas que se representan por medio de estas.
El plano de ejes más común es el cartesiano, idea del filósofo y matemático francés René Descartes.
Punto:
Un punto por definición carece de dimensiones y puede ser representado en un plano de ejes dando un valor en horizontal y otro en vertical.
Axioma:
En el plano existen infinitos puntos.
El valor en el plano horizontal se conoce como abscisa y el valor en el eje vertical se conoce como ordenada.
Representación en el plano:
\( A(x, y) \)
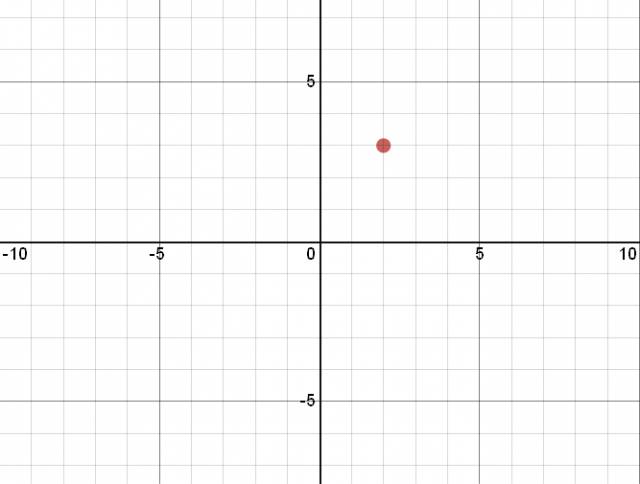
\( P(2, 3) ⇒ \) diremos que el punto llamado \( P \) tiene un valor de abscisa 2 y un valor de ordenada 3, y lo podemos graficar de la siguiente manera:
Recta:
Es la línea más corta que une dos puntos. Por un punto pasan infinitas rectas, pero por dos puntos pasa sólo una. Una recta está formada por infinitos puntos, no tiene comienzo ni fin, es infinita.
Toda línea recta puede ser representa por una ecuación lineal o de primer grado.
Formas de la ecuación de la recta:
1. La ecuación de la recta que pasa por el punto \( P_{1}(x_{1}, y_{1}) \) y cuya pendiente sea \( m \).
$$ y - y_{1} = m·(x - x_{1}) $$
2. Ecuación explícita de la recta: la ecuación de la recta de pendiente \( m \) y que corta al eje y en el punto \( (O, n) \), siendo \( n \) la ordenada en el origen.
$$ y = m·x + n $$
3. La ecuación de la recta que pasa por los puntos \( P_{1}(x_{1}, y_{1}) \) y \( P_{2}(x_{2}, y_{2}) \).
$$ \frac {y - y_{1}}{x - x_{1}} = \frac {y_{1} - y_{2}}{x_{1} - x_{2}} $$
4. La ecuación de la recta que corta a los ejes coordenados \( x \) e \( y \) en los puntos \( (a, O) \), siendo \( a \) la abscisa en el origen, y \( (O, b) \), siendo \( b \) la ordenada en el origen.
$$ \frac {x}{a} + \frac {y}{b} = 1 $$
5. Ecuación general de la recta: donde \( a, b, c \) son constantes arbitrarias que cumple que: su pendiente es \( m = - \frac {a}{b} \), y su ordenada en el origen es \( n = - \frac {c}{b} \).
$$ a·x + b·y + c = 0 $$
Si se conocen dos puntos, se pueden determinar \( a, b, c \) de la siguiente manera: \( a = y_{2} - y_{1}, b = x_{1} - x_{2}, c = x_{2}·y_{1} - x_{1}·y_{2} \).
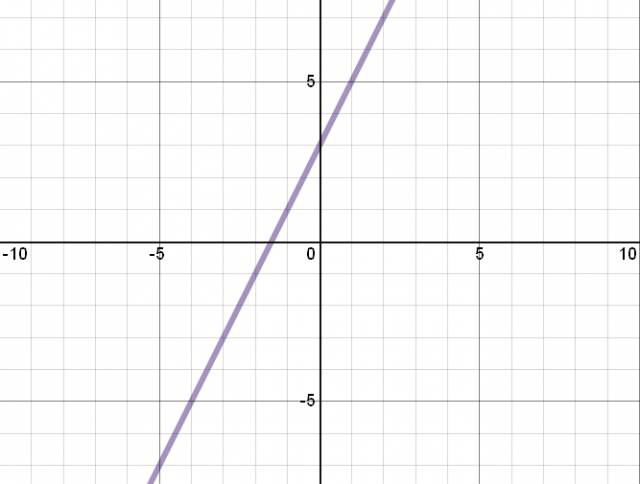
Representación gráfica en el plano:
Rectas paralelas:
Dos rectas son paralelas si tienen la misma pendiente.
$$ \begin{cases} r) y = m·x + n \\ s) y = m'·x + n' \end{cases} ⇒ r||s ⇔ m=m' $$
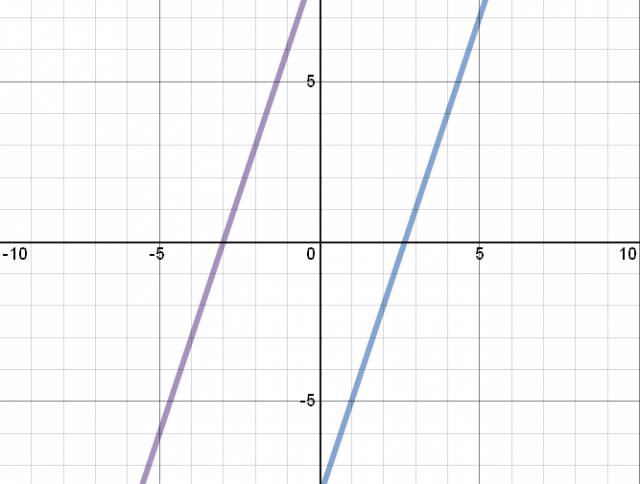
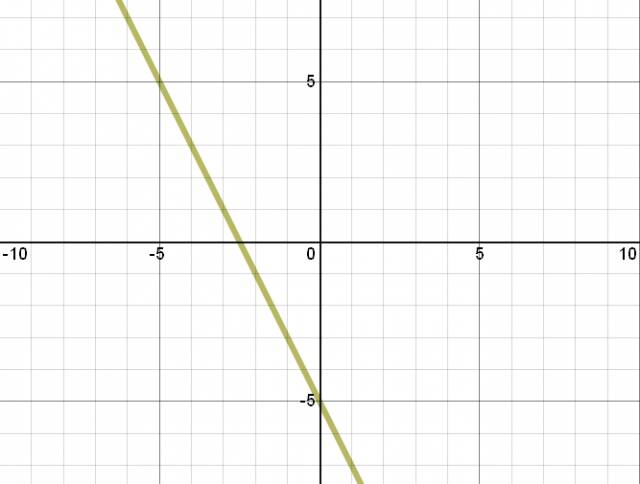
Las rectas que grafiqué fueron:
\( y = 3·x + 9 \)
\( y = 3·x - 8 \)
Rectas perpendiculares:
Dos rectas son perpendiculares si el producto de sus pendientes es -1, o sea, si una de las pendientes es opuesta e inversa a la otra.
$$ \begin{cases} r) y = m·x + n \\ s) y = m'·x + n' \end{cases} ⇒ r⊥s ⇔ m·m'=-1 $$
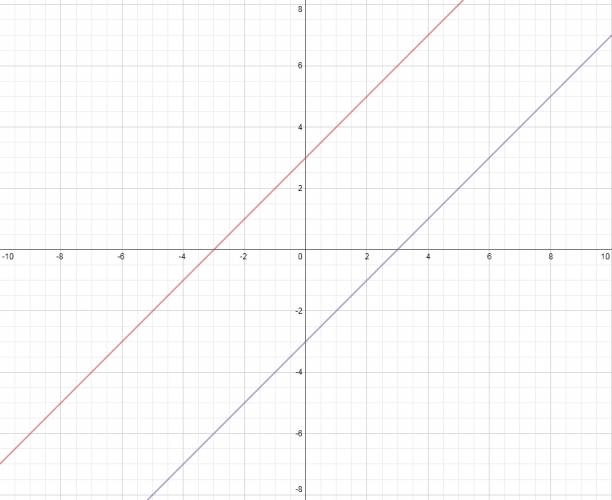
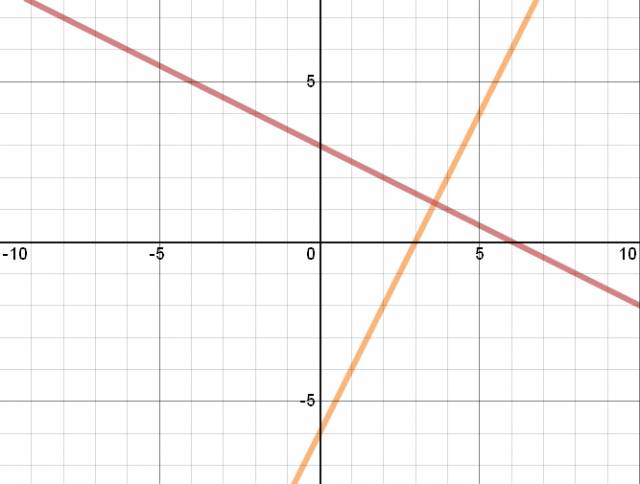
Las rectas que grafiqué fueron:
\( y = 2·x - 6 \)
\( y = -\frac {1}{2}·x + 3 \)
Fórmulas:
· Hallar recta que pasa por dos puntos:
$$ \frac {y - y_{1}}{x - x_{1}} = \frac {y_{1} - y_{2}}{x_{1} - x_{2}} $$
Condición: \( x_{A} ≠ x_{B} \)
· Hallar distancia entre dos puntos:
$$ d(A, B) = \sqrt {(x_{A} - x_{B})^2 +(y_{A} - y_{B})^2} $$
· Hallar distancia de un punto a una recta:
$$ d = \frac {|a·x+b·y+c|}{\sqrt{a^2 + b^2}} $$
Ver ejemplo
· Hallar distancia de una recta al origen de coordenadas:
$$ d = \frac {|c|}{\sqrt{a^2 + b^2}} $$
· Hallar punto medio entre dos puntos:
La abscisa del punto medio de otros dos, es la semisuma de sus abscisas; y la ordenada del punto medio de otros dos, es la semisuma de sus ordenadas.
$$ M \left( \frac {x_{A} + x_{B}}{2}; \frac {y_{A} + y_{B}}{2} \right) $$
El plano de ejes más común es el cartesiano, idea del filósofo y matemático francés René Descartes.
Punto:
Un punto por definición carece de dimensiones y puede ser representado en un plano de ejes dando un valor en horizontal y otro en vertical.
Axioma:
En el plano existen infinitos puntos.
El valor en el plano horizontal se conoce como abscisa y el valor en el eje vertical se conoce como ordenada.
Representación en el plano:
\( A(x, y) \)
\( P(2, 3) ⇒ \) diremos que el punto llamado \( P \) tiene un valor de abscisa 2 y un valor de ordenada 3, y lo podemos graficar de la siguiente manera:
Recta:
Es la línea más corta que une dos puntos. Por un punto pasan infinitas rectas, pero por dos puntos pasa sólo una. Una recta está formada por infinitos puntos, no tiene comienzo ni fin, es infinita.
Toda línea recta puede ser representa por una ecuación lineal o de primer grado.
Formas de la ecuación de la recta:
1. La ecuación de la recta que pasa por el punto \( P_{1}(x_{1}, y_{1}) \) y cuya pendiente sea \( m \).
$$ y - y_{1} = m·(x - x_{1}) $$
2. Ecuación explícita de la recta: la ecuación de la recta de pendiente \( m \) y que corta al eje y en el punto \( (O, n) \), siendo \( n \) la ordenada en el origen.
$$ y = m·x + n $$
3. La ecuación de la recta que pasa por los puntos \( P_{1}(x_{1}, y_{1}) \) y \( P_{2}(x_{2}, y_{2}) \).
$$ \frac {y - y_{1}}{x - x_{1}} = \frac {y_{1} - y_{2}}{x_{1} - x_{2}} $$
4. La ecuación de la recta que corta a los ejes coordenados \( x \) e \( y \) en los puntos \( (a, O) \), siendo \( a \) la abscisa en el origen, y \( (O, b) \), siendo \( b \) la ordenada en el origen.
$$ \frac {x}{a} + \frac {y}{b} = 1 $$
5. Ecuación general de la recta: donde \( a, b, c \) son constantes arbitrarias que cumple que: su pendiente es \( m = - \frac {a}{b} \), y su ordenada en el origen es \( n = - \frac {c}{b} \).
$$ a·x + b·y + c = 0 $$
Si se conocen dos puntos, se pueden determinar \( a, b, c \) de la siguiente manera: \( a = y_{2} - y_{1}, b = x_{1} - x_{2}, c = x_{2}·y_{1} - x_{1}·y_{2} \).
Representación gráfica en el plano:
Rectas paralelas:
Dos rectas son paralelas si tienen la misma pendiente.
$$ \begin{cases} r) y = m·x + n \\ s) y = m'·x + n' \end{cases} ⇒ r||s ⇔ m=m' $$
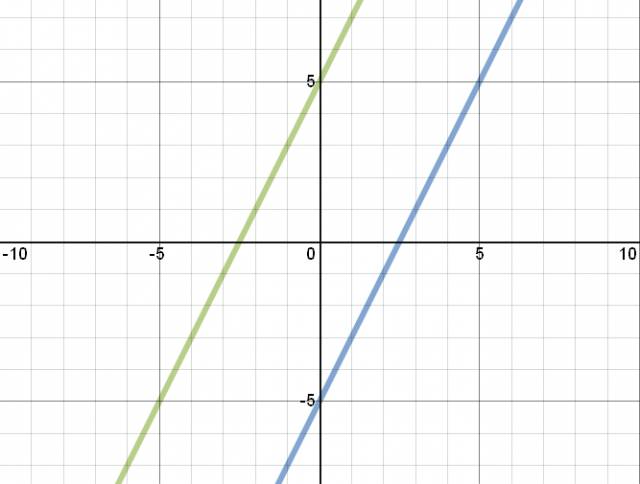
Las rectas que grafiqué fueron:
\( y = 3·x + 9 \)
\( y = 3·x - 8 \)
Rectas perpendiculares:
Dos rectas son perpendiculares si el producto de sus pendientes es -1, o sea, si una de las pendientes es opuesta e inversa a la otra.
$$ \begin{cases} r) y = m·x + n \\ s) y = m'·x + n' \end{cases} ⇒ r⊥s ⇔ m·m'=-1 $$
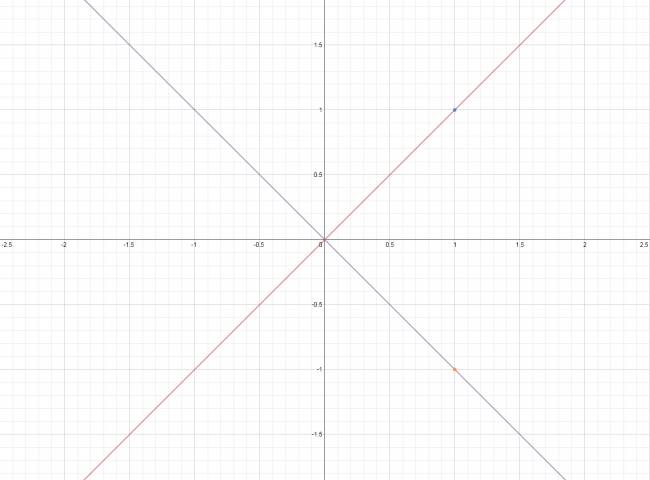
Demostración de la condición de perpendicularidad
Sean:
\( (t) y = m·x \)
\( (p) y = m'·x \)
Sean \( P \) y \( Q \) los puntos de abscisa 1 que pertenecen a \( (t) \) y \( (p) \) respectivamente. Entonces:
$$ (t) y=m·x ⇒ y = m·1 ⇒ y = m ⇒ P (1,m) $$
$$ (p) y=m'·x ⇒ y = m'·1 ⇒ y = m' ⇒ Q (1,m') $$
Aplicando el teorema de Pitágoras en OPQ tenemos que:
$$ \overline {PQ}^2 = \overline {OP}^2 + \overline {OQ}^2 $$
$$ (\sqrt {(m'-m)^2 + (1-1)^2})^2 = (\sqrt {(m-0)^2 + (1-0)^2})^2 + (\sqrt {(m'-0)^2 + (1-0)^2})^2 $$
$$ 0^2 + (m'-m)^2 = m^2 + 1^2 + m'^2 + 1^2 $$
$$ m'^2 - 2·m·m' + m^2 = m^2 + m'^2 + 2 $$
$$ -2·m·m' = 2 ⇔ m·m' = -1 ∎ $$
Sean:
\( (t) y = m·x \)
\( (p) y = m'·x \)
Sean \( P \) y \( Q \) los puntos de abscisa 1 que pertenecen a \( (t) \) y \( (p) \) respectivamente. Entonces:
$$ (t) y=m·x ⇒ y = m·1 ⇒ y = m ⇒ P (1,m) $$
$$ (p) y=m'·x ⇒ y = m'·1 ⇒ y = m' ⇒ Q (1,m') $$
Aplicando el teorema de Pitágoras en OPQ tenemos que:
$$ \overline {PQ}^2 = \overline {OP}^2 + \overline {OQ}^2 $$
$$ (\sqrt {(m'-m)^2 + (1-1)^2})^2 = (\sqrt {(m-0)^2 + (1-0)^2})^2 + (\sqrt {(m'-0)^2 + (1-0)^2})^2 $$
$$ 0^2 + (m'-m)^2 = m^2 + 1^2 + m'^2 + 1^2 $$
$$ m'^2 - 2·m·m' + m^2 = m^2 + m'^2 + 2 $$
$$ -2·m·m' = 2 ⇔ m·m' = -1 ∎ $$
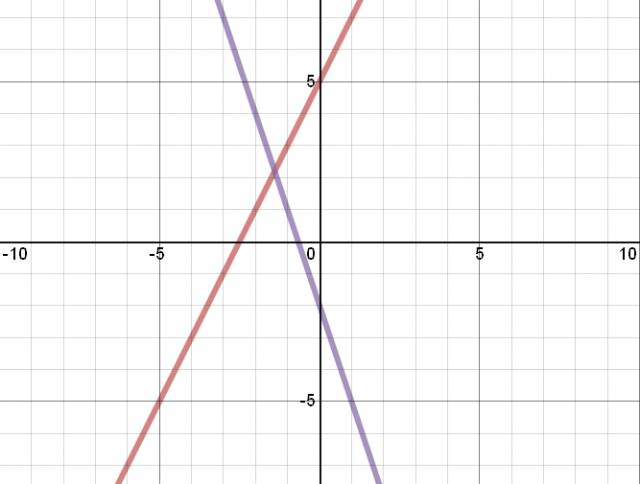
Las rectas que grafiqué fueron:
\( y = 2·x - 6 \)
\( y = -\frac {1}{2}·x + 3 \)
Fórmulas:
· Hallar recta que pasa por dos puntos:
$$ \frac {y - y_{1}}{x - x_{1}} = \frac {y_{1} - y_{2}}{x_{1} - x_{2}} $$
Condición: \( x_{A} ≠ x_{B} \)
· Hallar distancia entre dos puntos:
$$ d(A, B) = \sqrt {(x_{A} - x_{B})^2 +(y_{A} - y_{B})^2} $$
· Hallar distancia de un punto a una recta:
$$ d = \frac {|a·x+b·y+c|}{\sqrt{a^2 + b^2}} $$
Ver ejemplo
Se consideran dos puntos de diferente abscisa y diferente ordenada.
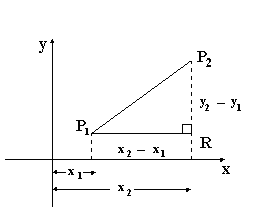
Como se ve en la imagen, esto genera un triángulo rectángulo (ya que los ejes cartesianos son perpendiculares entre sí), al ser un triángulo rectángulo y lo que queremos calcular es su hipotenusa, escribimos el teorema de Pitágoras para conocer su hipotenusa.
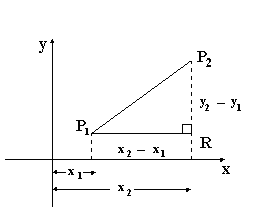
Como se ve en la imagen, esto genera un triángulo rectángulo (ya que los ejes cartesianos son perpendiculares entre sí), al ser un triángulo rectángulo y lo que queremos calcular es su hipotenusa, escribimos el teorema de Pitágoras para conocer su hipotenusa.
· Hallar distancia de una recta al origen de coordenadas:
$$ d = \frac {|c|}{\sqrt{a^2 + b^2}} $$
· Hallar punto medio entre dos puntos:
La abscisa del punto medio de otros dos, es la semisuma de sus abscisas; y la ordenada del punto medio de otros dos, es la semisuma de sus ordenadas.
$$ M \left( \frac {x_{A} + x_{B}}{2}; \frac {y_{A} + y_{B}}{2} \right) $$