23-10-2012, 5:21 PM
Es un teorema matemático que establece una igualdad entre los catetos y la hipotenusa en los triángulos rectángulos, este teorema le es atribuido a Pitágoras de Samos aunque él no lo descubrió, sino que fue un discípulo suyo el que lo hizo. De todos modos se sabe que su descubrimiento fue anterior al de Pitágoras y su escuela, ya que en China entre los años 500 y el 300 a. C. se publicó una obra matemática conocida como Chou Pei donde aparecía la demostración de este teorema.
Enunciado:
"En todo triángulo rectángulo se sabe que la suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa."
Siendo:
· Los catetos: los lados más cortos.
· La hipotenusa: los lados más largos.
Expresión matemática:

Teorema de Pitágoras por calculadora científica:
Si queremos hallar la hipotenusa de un triángulo rectángulo cuyos catetos miden 3 y 4 aplicamos el teorema de Pitágoras, podrías hacer las cuentas raíz cuadrada de la suma de los cuadrados de los catetos y llegaríamos al valor de la hipotenusa, resulta que algunas calculadoras cuentan con la función Pol, lo cual simplifica las cosas, basta con introducir los valores de los catetos y nos dirá el valor de la hipotenusa, la sintaxis es la siguiente:
Pol(3,4) lo cual nos devolverá el valor 5.
· La calculador científica CASIO fx-95MS cuenta con esta función.

Ternas pitagóricas:
Existen ternas pitagóricas ya documentadas, por ejemplo:
$$ cat_{1} = 3, cat_{2} = 4, hip = 5 $$
Recíproco del teorema de Pitágoras:
En todo triángulo que se cumpla que el cuadrado del lado mayor sea igual a la suma de los cuadrados de los otros dos lados, afirmaremos que el triángulo es cuestión es rectángulo.
Enunciado:
"En todo triángulo rectángulo se sabe que la suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa."
Siendo:
· Los catetos: los lados más cortos.
· La hipotenusa: los lados más largos.
Expresión matemática:

Cita
Demostración gráfica:
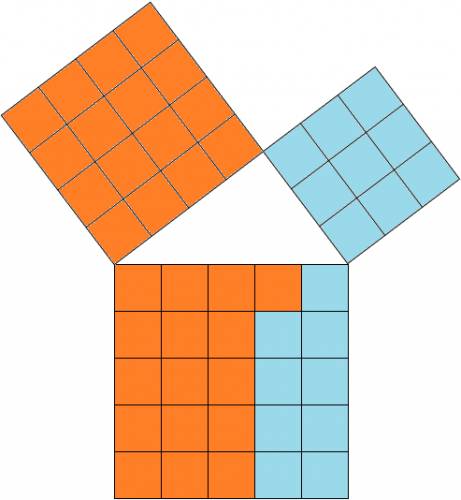
Demostración analítica:
Ver demostración: http://www.x.edu.uy/teoremapi.swf
· Este teorema en particular tienen cientos de demostraciones registradas.

Demostración analítica:
Ver demostración: http://www.x.edu.uy/teoremapi.swf
· Este teorema en particular tienen cientos de demostraciones registradas.
Teorema de Pitágoras por calculadora científica:
Si queremos hallar la hipotenusa de un triángulo rectángulo cuyos catetos miden 3 y 4 aplicamos el teorema de Pitágoras, podrías hacer las cuentas raíz cuadrada de la suma de los cuadrados de los catetos y llegaríamos al valor de la hipotenusa, resulta que algunas calculadoras cuentan con la función Pol, lo cual simplifica las cosas, basta con introducir los valores de los catetos y nos dirá el valor de la hipotenusa, la sintaxis es la siguiente:
Pol(3,4) lo cual nos devolverá el valor 5.
· La calculador científica CASIO fx-95MS cuenta con esta función.

Ternas pitagóricas:
Existen ternas pitagóricas ya documentadas, por ejemplo:
$$ cat_{1} = 3, cat_{2} = 4, hip = 5 $$
Recíproco del teorema de Pitágoras:
En todo triángulo que se cumpla que el cuadrado del lado mayor sea igual a la suma de los cuadrados de los otros dos lados, afirmaremos que el triángulo es cuestión es rectángulo.