23-10-2012, 5:08 PM
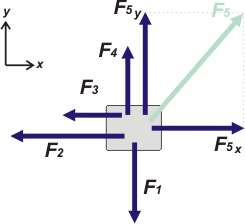
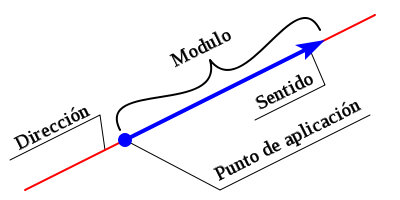
Una fuerzas es una magnitud vectorial, por lo que tiene: punto de aplicación, dirección, sentido y módulo.
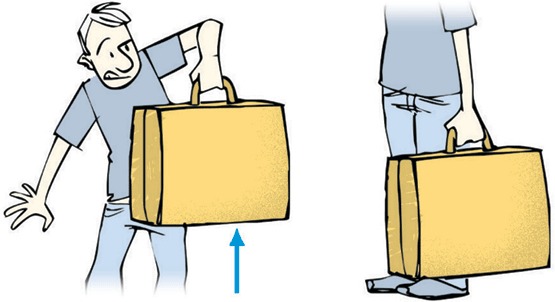
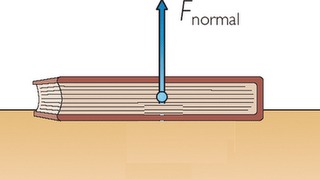
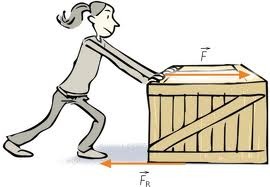
Por ejemplo, ejercemos una fuerza sobre un objeto para levantarlo:
Suma de vectores colineales:
Los vectores colineales son aquellos que tienen la misma dirección.
· Suma de vectores colineales de igual sentido:
Se suman los módulos de los vectores, el vector resultante es un vector cuyo módulo es la suma de ambos y tiene igual dirección, sentido y punto de aplicación.
· Suma de vectores colineales de diferente sentido:
Se restan los módulos de los vectores, el vector resultante es un vector cuyo módulo es la resta de ambos y tiene igual dirección, sentido opuesto y mismo punto de aplicación.
Suma de vectores no-colineales:
Los vectores no-colineales son aquellos que no tienen la misma dirección.
· Suma de vectores no-colineales perpendiculares entre sí:
Basta con aplicar Pitágoras para conocer su módulo.
· Suma de vectores no-colineales no-perpendiculares entre sí:
Se deberá aplicar el teorema del seno y/o del coseno. Su representación se puede realizar a través del método del paralelogramo, y si se tratase de más de dos fuerzas, se deberá emplear el método de la poligonal.
Método del paralelogramo:
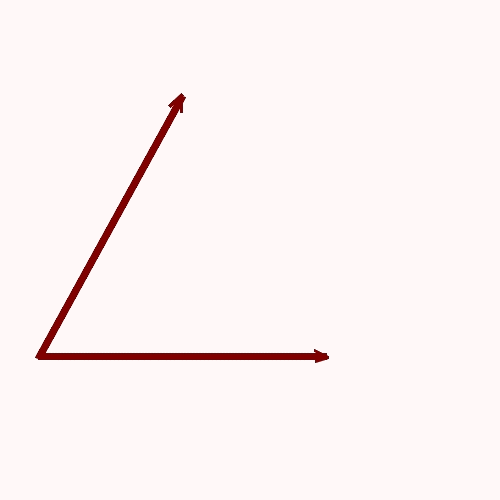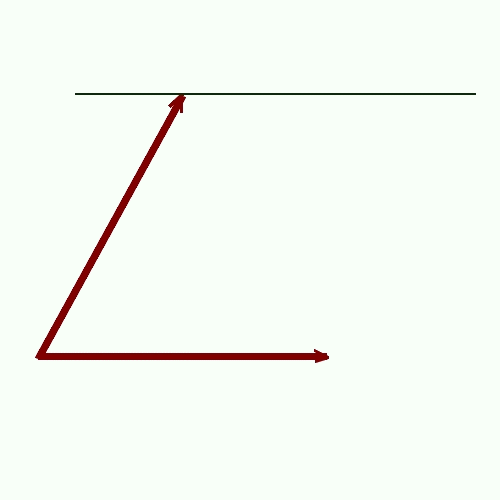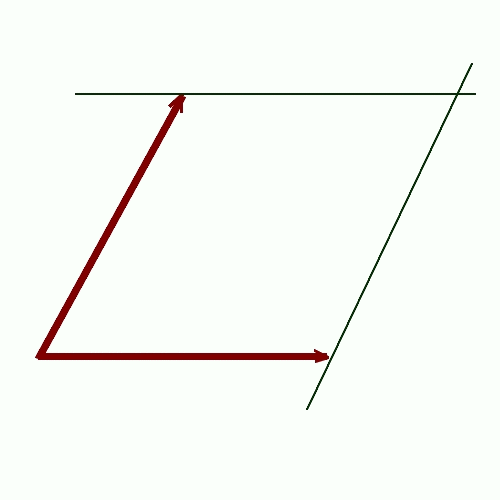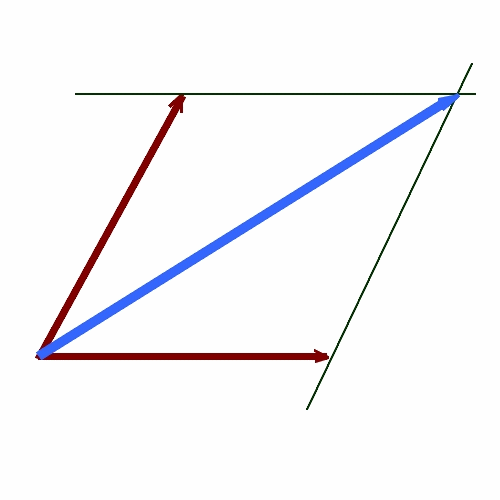
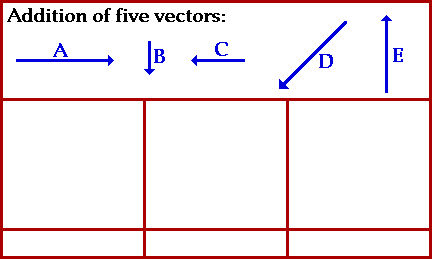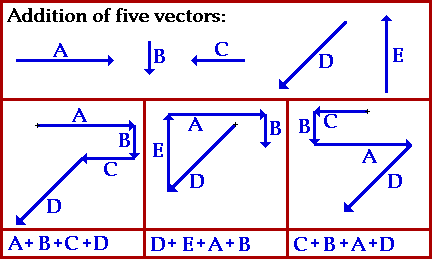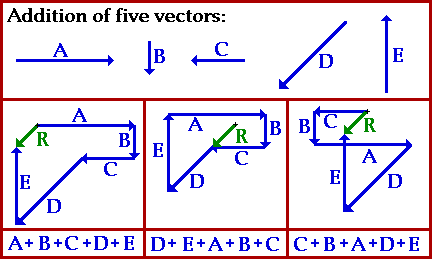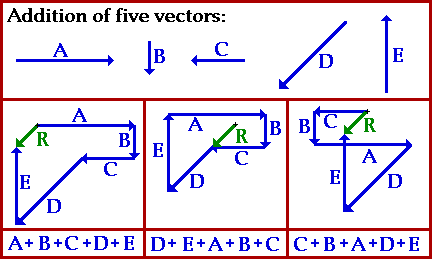
Método de la poligonal:
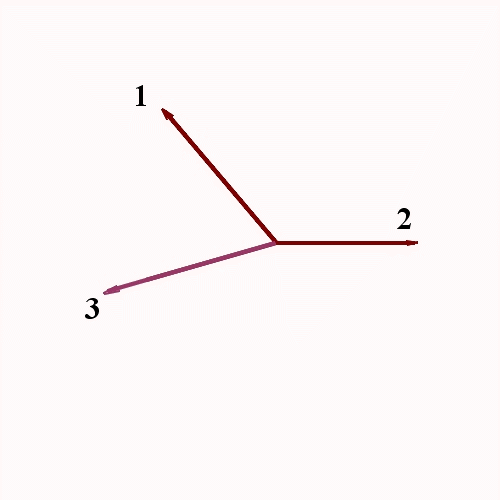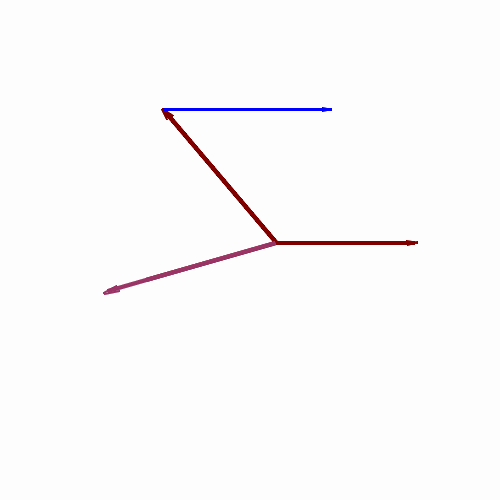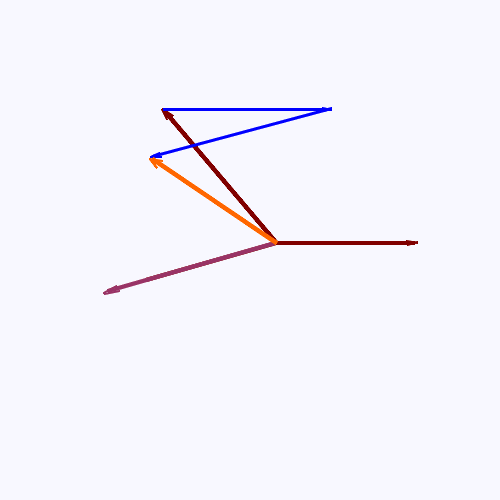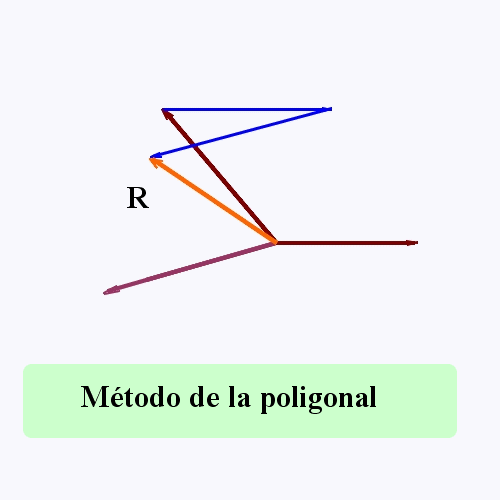
Recordar que la suma de vectores es conmutativa:
Por ejemplo, ejercemos una fuerza sobre un objeto para levantarlo:
Suma de vectores colineales:
Los vectores colineales son aquellos que tienen la misma dirección.
· Suma de vectores colineales de igual sentido:
Se suman los módulos de los vectores, el vector resultante es un vector cuyo módulo es la suma de ambos y tiene igual dirección, sentido y punto de aplicación.
· Suma de vectores colineales de diferente sentido:
Se restan los módulos de los vectores, el vector resultante es un vector cuyo módulo es la resta de ambos y tiene igual dirección, sentido opuesto y mismo punto de aplicación.
Suma de vectores no-colineales:
Los vectores no-colineales son aquellos que no tienen la misma dirección.
· Suma de vectores no-colineales perpendiculares entre sí:
Basta con aplicar Pitágoras para conocer su módulo.
· Suma de vectores no-colineales no-perpendiculares entre sí:
Se deberá aplicar el teorema del seno y/o del coseno. Su representación se puede realizar a través del método del paralelogramo, y si se tratase de más de dos fuerzas, se deberá emplear el método de la poligonal.
Método del paralelogramo:
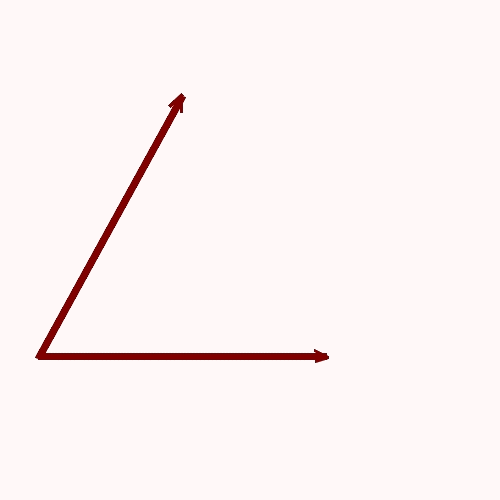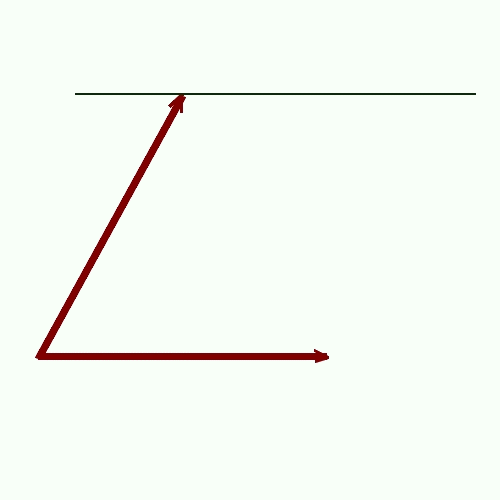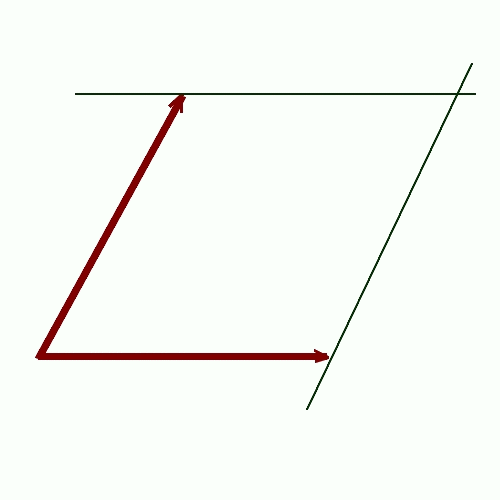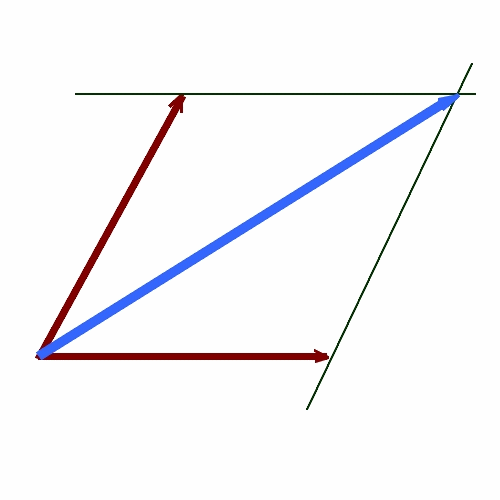
Método de la poligonal:
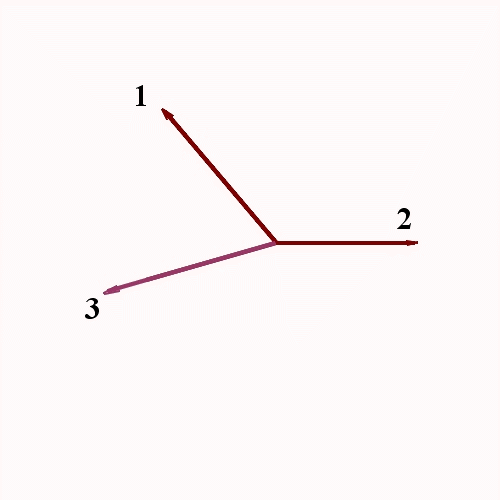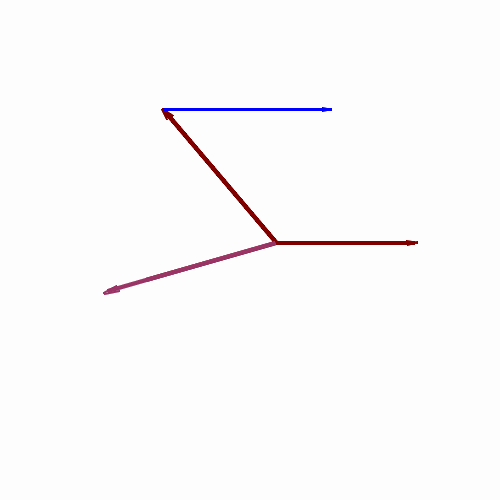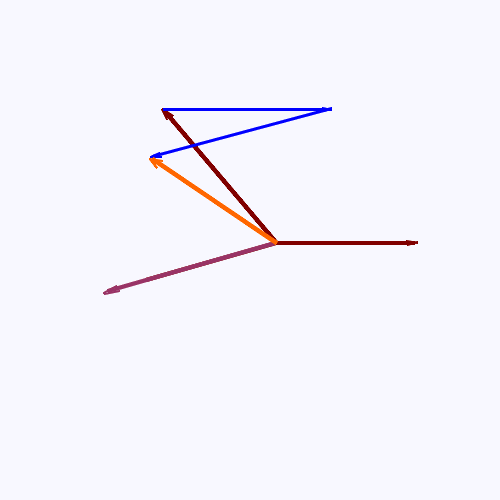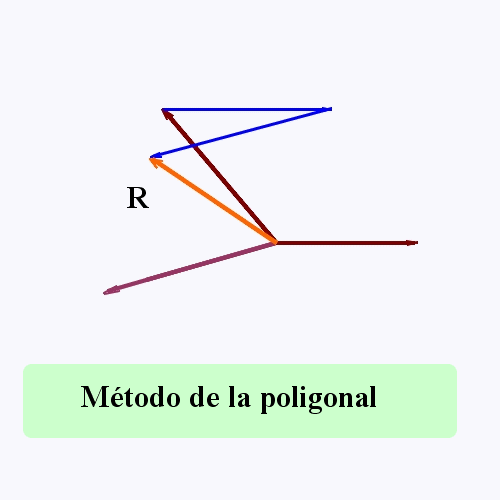
Recordar que la suma de vectores es conmutativa:
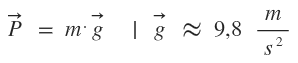
jaja esta muy buena las definiciones.... ahora voy a tratar de hacer un ejercicioo
