08-08-2013, 1:28 AM
Hallar las nuevas coordenadas de un punto fijo, luego de haber realizado una traslación de ejes
Aplicarle una traslación de ejes a un sistema cartesiano \( x,y \) implica trasladar paralelamente sus ejes hasta el nuevo origen que le llamamos \( O' (x_{o}, y_{o}) \).
La idea con esta propiedad es establecer la relación que existe entre las viejas coordenadas y las nuevas.
Sea:
\( P (x, y) \) un punto cualquiera del plano.
\( P (x', y') \) coordenadas de P en el sistema cartesiano.
Condición de traslación de ejes:
$$ x = x_{o} + x' $$
$$ y = y_{o} + y' $$
Esta relación se cumple con P en cualquiera de los cuatro cuadrantes.
Aplicarle una traslación de ejes a un sistema cartesiano \( x,y \) implica trasladar paralelamente sus ejes hasta el nuevo origen que le llamamos \( O' (x_{o}, y_{o}) \).
La idea con esta propiedad es establecer la relación que existe entre las viejas coordenadas y las nuevas.
Sea:
\( P (x, y) \) un punto cualquiera del plano.
\( P (x', y') \) coordenadas de P en el sistema cartesiano.
Condición de traslación de ejes:
$$ x = x_{o} + x' $$
$$ y = y_{o} + y' $$
Esta relación se cumple con P en cualquiera de los cuatro cuadrantes.
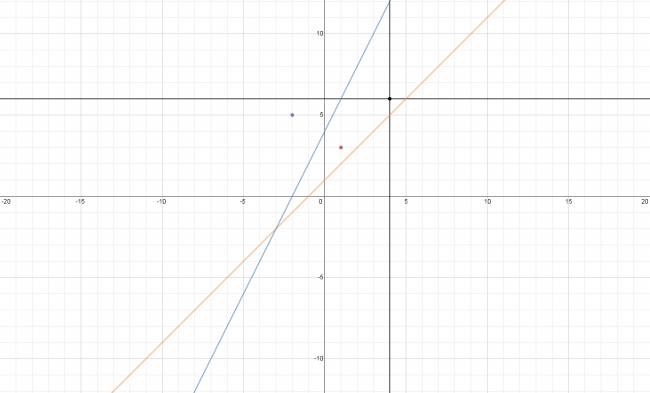
Dados:
\( A (1, 3) \)
\( B (-2, 5) \)
\( ( r ) y = x + 1 \)
\( (s) 2·x - y + 4 = 0 \)
Indicar los puntos y rectas anteriores, efectuando una traslación de ejes con nuevo origen \( O' (4, 6) \).
Puntos:
\( A (1, 3) → A (1-4, 3-6) → A (-3, -3) \)
\( B (-2, 5) → A (-2-4, 5-6) → A (-6, -1) \)
Rectas:
\( ( r ) y = x + 1 → 4·x' = 6 + y' + 5 → y' = x' - 1 \)
\( (s) 2·x - y + 4 = 0 → 2·x' - y' + 6 = 0 \)
\( A (1, 3) \)
\( B (-2, 5) \)
\( ( r ) y = x + 1 \)
\( (s) 2·x - y + 4 = 0 \)
Indicar los puntos y rectas anteriores, efectuando una traslación de ejes con nuevo origen \( O' (4, 6) \).
Puntos:
\( A (1, 3) → A (1-4, 3-6) → A (-3, -3) \)
\( B (-2, 5) → A (-2-4, 5-6) → A (-6, -1) \)
Rectas:
\( ( r ) y = x + 1 → 4·x' = 6 + y' + 5 → y' = x' - 1 \)
\( (s) 2·x - y + 4 = 0 → 2·x' - y' + 6 = 0 \)