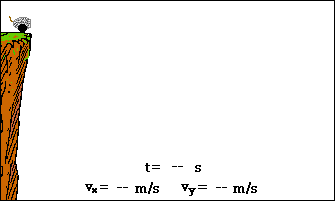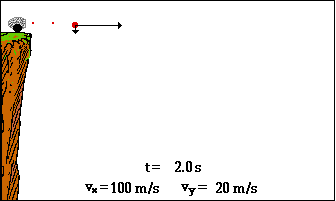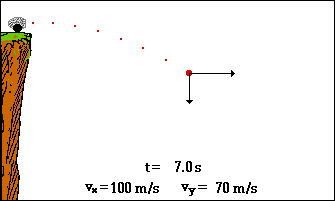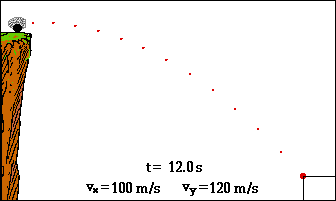22-10-2012, 8:03 PM
También conocido como lanzamiento de proyectiles o tiro parabólico es un tipo de movimiento variado que actúa en dos dimensiones.
Este tipo de movimiento se produce cuando se lanza un objeto en un ángulo menor a 90º y mayor a 0º. Llamaremos α a este ángulo de inclinación. Diremos que 0º<α<90º. Se dice que es un movimiento compuesto, porque, a diferencia caída libre: un objeto se deja caer o se lanza hacia arriba, donde el desplazamiento es nulo pero la altura es variable, y cuando, por ejemplo, un auto viaja por la carretera, este no salta por la carretera, sino que viaja por esta, esto significa que la altura es constante mientras que el desplazamiento es variable. Para representar los anteriores sistemas no se necesita más de un eje, pero para este tema necesitaremos los dos ejes: el horizontal y el vertical.
Aceptaremos la siguiente premisa: “todos los objetos que son lanzados con un ángulo α, describen una parábola con su trayectoria”. Esto significa lo siguiente:
Para hacer referencia a un momento indicado del cuerpo necesitaríamos ver a qué distancia de altura y a qué distancia en horizontal -desde un punto arbitrario- están.
La única fuerza que actúa sobre el cuerpo es el peso: P.
Aceptaremos la siguiente premisa: “la velocidad del cuerpo en la altura máxima será 0”.
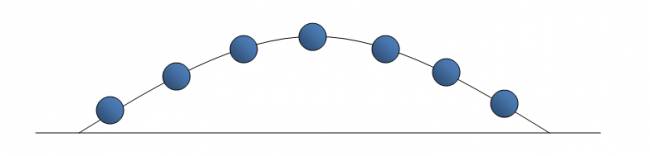
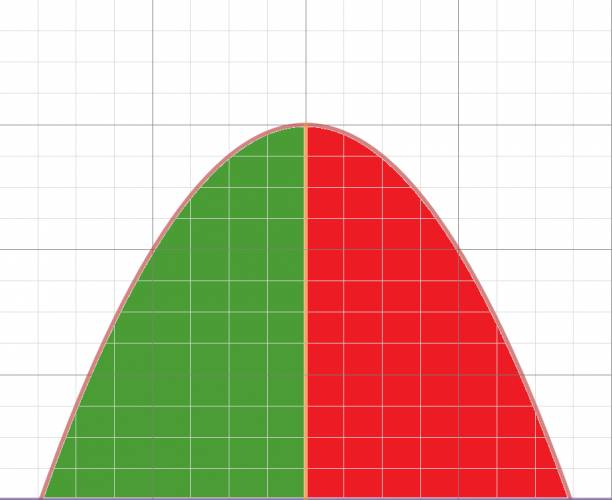
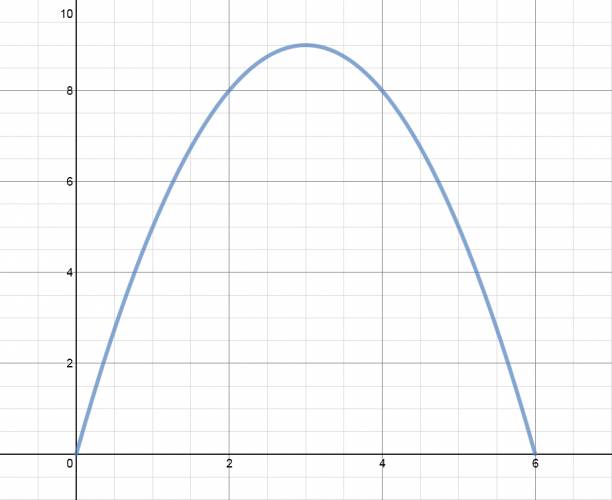
Las velocidades del cuerpo a través de la parábola van variando. Podemos dividir a la parábola en dos mitades exactas:
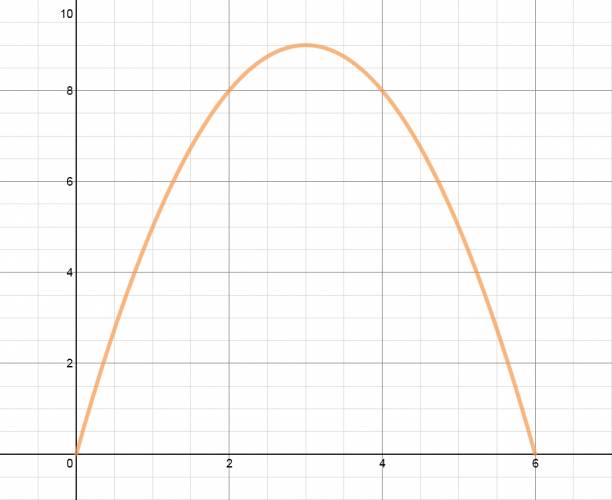
La altura máxima se encuentra representada en naranja, en la figura superior.
Las velocidades en la primera mitad de la parábola son positivas, pero van disminuyendo. Las velocidades en la segunda mitad de la parábola son negativas, pero van aumentado.
Aceptaremos la siguiente premisa: “si el cuerpo se lanza y cae a la misma altura, entonces, la altura máxima del objeto se encuentra en la mitad exacta de la parábola, y también se cumple que la mitad del tiempo que permanece en el aire, es el tiempo que demora en llegar a la altura máxima”.
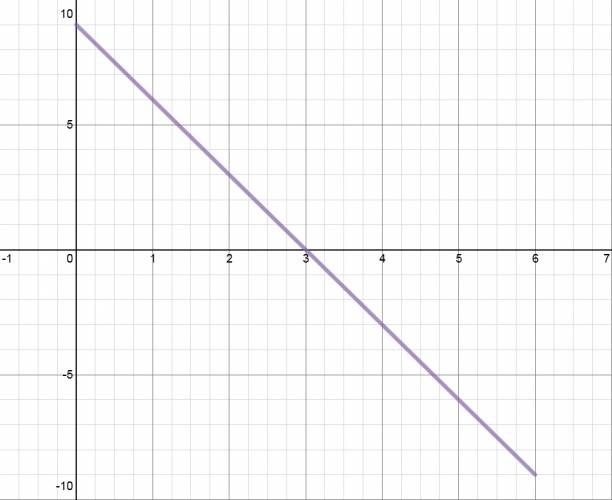
La trayectoria del cuerpo describe una parábola, se puede conocer la velocidad del cuerpo en cada punto de la parábola, pero la mayoría del tiempo tendremos vectores inclinados de la velocidad:
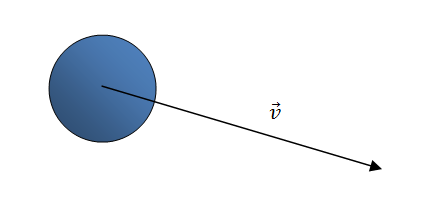
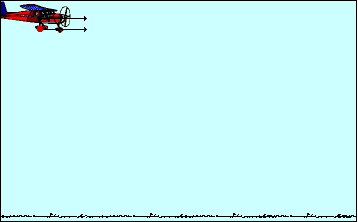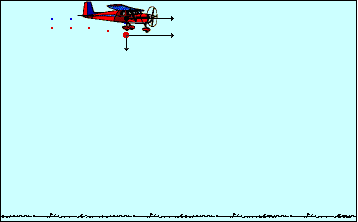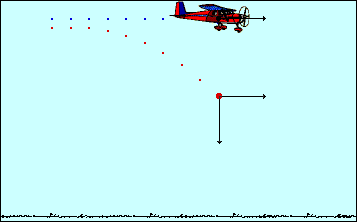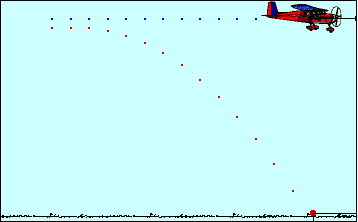
Pero debemos descomponer la velocidad en ambos ejes: tanto vertical como horizontal.
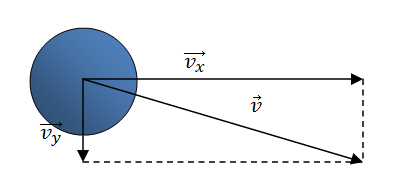
Está demostrado que en el eje horizontal, los cuerpos se mueven con M.R.U.; mientras que en el eje vertical se mueven con M.R.U.V.
Por esta razón, para predecir su movimiento utilizaremos las fórmulas de los movimientos mencionados.
Fórmulas:
Análisis del movimiento:
Este tipo de movimiento se produce cuando se lanza un objeto en un ángulo menor a 90º y mayor a 0º. Llamaremos α a este ángulo de inclinación. Diremos que 0º<α<90º. Se dice que es un movimiento compuesto, porque, a diferencia caída libre: un objeto se deja caer o se lanza hacia arriba, donde el desplazamiento es nulo pero la altura es variable, y cuando, por ejemplo, un auto viaja por la carretera, este no salta por la carretera, sino que viaja por esta, esto significa que la altura es constante mientras que el desplazamiento es variable. Para representar los anteriores sistemas no se necesita más de un eje, pero para este tema necesitaremos los dos ejes: el horizontal y el vertical.
Aceptaremos la siguiente premisa: “todos los objetos que son lanzados con un ángulo α, describen una parábola con su trayectoria”. Esto significa lo siguiente:
Para hacer referencia a un momento indicado del cuerpo necesitaríamos ver a qué distancia de altura y a qué distancia en horizontal -desde un punto arbitrario- están.
La única fuerza que actúa sobre el cuerpo es el peso: P.
Aceptaremos la siguiente premisa: “la velocidad del cuerpo en la altura máxima será 0”.
Las velocidades del cuerpo a través de la parábola van variando. Podemos dividir a la parábola en dos mitades exactas:
La altura máxima se encuentra representada en naranja, en la figura superior.
Las velocidades en la primera mitad de la parábola son positivas, pero van disminuyendo. Las velocidades en la segunda mitad de la parábola son negativas, pero van aumentado.
Aceptaremos la siguiente premisa: “si el cuerpo se lanza y cae a la misma altura, entonces, la altura máxima del objeto se encuentra en la mitad exacta de la parábola, y también se cumple que la mitad del tiempo que permanece en el aire, es el tiempo que demora en llegar a la altura máxima”.
La trayectoria del cuerpo describe una parábola, se puede conocer la velocidad del cuerpo en cada punto de la parábola, pero la mayoría del tiempo tendremos vectores inclinados de la velocidad:
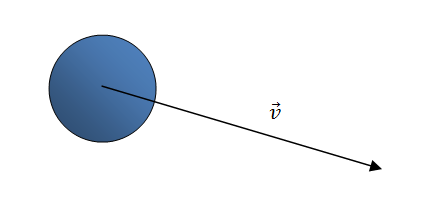
Pero debemos descomponer la velocidad en ambos ejes: tanto vertical como horizontal.

Está demostrado que en el eje horizontal, los cuerpos se mueven con M.R.U.; mientras que en el eje vertical se mueven con M.R.U.V.
Por esta razón, para predecir su movimiento utilizaremos las fórmulas de los movimientos mencionados.
Fórmulas:
Cita
$$ v_{oy} = v_{o}·\mbox{sen} \alpha $$
$$ v_{ox} = v_{o}·\cos \alpha $$
$$ v_{ox} = v_{x} $$
$$ \Delta y = v_{oy}· \Delta t - \frac {g· \Delta t^2}{2} $$
$$ v_{y} = v_{oy} - g· \Delta t $$
$$ v_{x} = \frac {\Delta x}{\Delta t} $$
$$ \Delta t_{PARCIAL} = \frac {v_{oy}}{g} $$
$$ \Delta t_{TOTAL} = \frac {2·v_{oy}}{g} $$
$$ tg \alpha = \frac {v_{oy}}{v_{ox}} $$
$$ \Delta y = \frac {(v_{o}·sen \alpha)^2}{2·g} = \frac {(v_{oy})^2}{2·g} $$
$$ \Delta t = \sqrt{\frac {2· \Delta y}{g}} $$
$$ \Delta y = tg \alpha · \Delta x - g· \frac{\Delta t^2}{2·(v_{o}·cos \alpha)} $$
$$ v_{ox} = v_{o}·\cos \alpha $$
$$ v_{ox} = v_{x} $$
$$ \Delta y = v_{oy}· \Delta t - \frac {g· \Delta t^2}{2} $$
$$ v_{y} = v_{oy} - g· \Delta t $$
$$ v_{x} = \frac {\Delta x}{\Delta t} $$
$$ \Delta t_{PARCIAL} = \frac {v_{oy}}{g} $$
$$ \Delta t_{TOTAL} = \frac {2·v_{oy}}{g} $$
$$ tg \alpha = \frac {v_{oy}}{v_{ox}} $$
$$ \Delta y = \frac {(v_{o}·sen \alpha)^2}{2·g} = \frac {(v_{oy})^2}{2·g} $$
$$ \Delta t = \sqrt{\frac {2· \Delta y}{g}} $$
$$ \Delta y = tg \alpha · \Delta x - g· \frac{\Delta t^2}{2·(v_{o}·cos \alpha)} $$
Análisis del movimiento: