04-07-2013, 0:50 AM
Esta ley física fue determinada en 1826 por Georg Ohm, físico y matemático alemán.
Enunciado:
La intensidad de corriente que circula por el conductor es directamente proporcional a la diferencia de potencial entre los extremos del conductor e inversamente proporcional a la resistencia del conductor.
Expresión matemática:
$$ R = \frac {V}{I} \left [ Ω = \frac {V}{A} \right ] $$
Referencias:
· R = resistencia, se mide en ohmios (Ω).
· I = intensidad, se mide en amperios (A).
· V = diferencia de potencial, se mide en voltios (V).
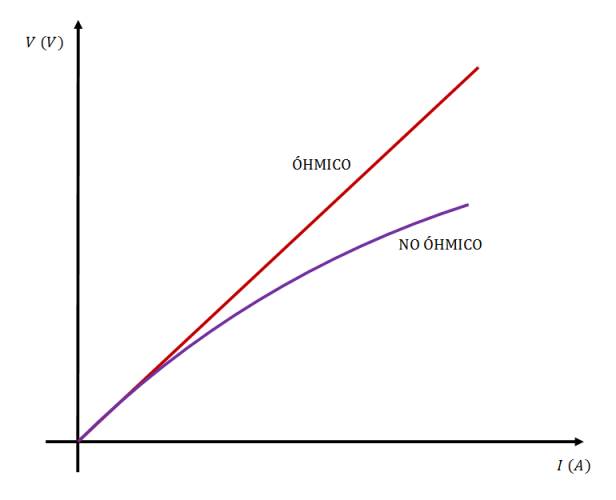
Gráfico:
En el caso de que sea un conductor óhmico, se puede calcular su resistencia a través de la ley de Ohm o calculando la pendiente del gráfico (que es lo mismo que la fórmula de la ley).
· Para calcular su resistencia:
$$ p = \frac {\Delta y}{\Delta x} = \frac {V}{I} = R $$
· Para calcular la incertidumbre (por teorema de propagación de errores):
$$ δR = R· \left( \frac {δV}{V} + \frac {δI}{I} \right) $$
· Correcta expresión de la resistencia de un conductor óhmico:
$$ R = \left( R_{A} ± δR_{A} \right) Ω $$
Enunciado:
La intensidad de corriente que circula por el conductor es directamente proporcional a la diferencia de potencial entre los extremos del conductor e inversamente proporcional a la resistencia del conductor.
Expresión matemática:
$$ R = \frac {V}{I} \left [ Ω = \frac {V}{A} \right ] $$
Referencias:
· R = resistencia, se mide en ohmios (Ω).
· I = intensidad, se mide en amperios (A).
· V = diferencia de potencial, se mide en voltios (V).
Gráfico:
En el caso de que sea un conductor óhmico, se puede calcular su resistencia a través de la ley de Ohm o calculando la pendiente del gráfico (que es lo mismo que la fórmula de la ley).
· Para calcular su resistencia:
$$ p = \frac {\Delta y}{\Delta x} = \frac {V}{I} = R $$
· Para calcular la incertidumbre (por teorema de propagación de errores):
$$ δR = R· \left( \frac {δV}{V} + \frac {δI}{I} \right) $$
· Correcta expresión de la resistencia de un conductor óhmico:
$$ R = \left( R_{A} ± δR_{A} \right) Ω $$