01-07-2013, 1:49 PM
Coordenadas polares: introducción
Para conocer este sistema debemos haber trabajado el sistema de ejes cartesianos (el formado por dos rectas perpendiculares).
Repaso del sistema de ejes cartesianos:
Si recordamos, cuando trabajamos con este sistema decíamos: "puedo representar cualquier punto del plano dándole un valor en horizontal y otro en vertical".
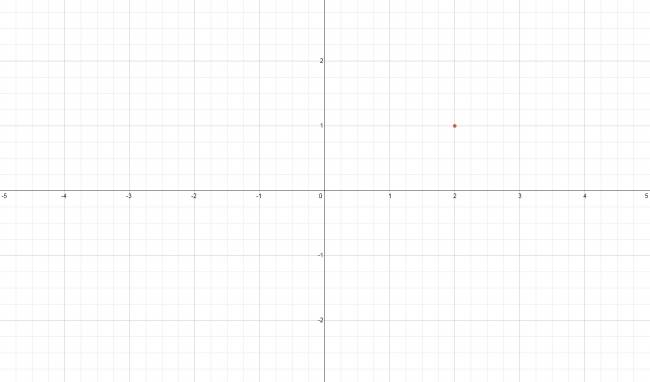
Como vemos, grafiqué un punto que tiene coordenadas: 2 en horizontal y 1 en vertical. La notación que usábamos era la siguiente: \( P (2,1) \)
Como siempre digo: \( P \) es para dar un nombre, y generalmente uso tal letra ya que es la inicial de punto.
Ahora sí volvemos a lo que queríamos: coordenadas polares
Las coordenadas polares dicen algo como esto: "puedo representar cualquier punto del plano dándole una distancia de separación con respecto al origen, y la inclinación que este posee". ¡No colapses que ahora explico!
Imaginá un punto fijo, le vas a llamar origen de coordenadas, lo voy a representar con rojo, y ahora quiero que imagine un punto que no sea el anterior, lo voy a representar con anaranjado.
Acá una imagen para que no te pierdas imaginando:
Ahora vamos a trazar un segmento que una ambos puntos:
Ahora me pregunto, la distancia de separación entre el origen y el punto que elegí, ¿es única? No dudes, ¡decí que no!
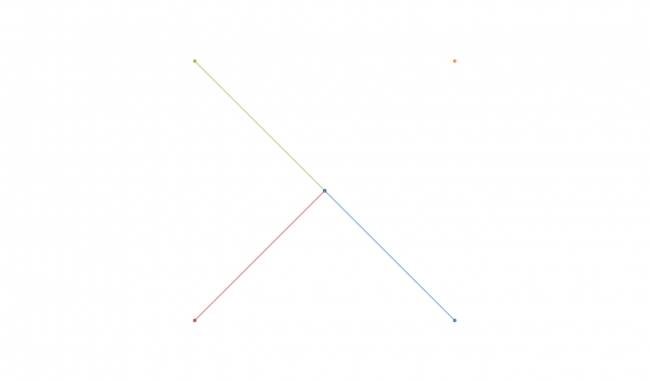
Suponé estos casos:
Ahí dibujé tres casos, pero podría haber dibujado infinitos segmentos que cumplían la condición de que tenían la misma distancia de separación con en el origen, la cosa es que ese segmento solo no me está diciendo mucho del punto que hace un rato había elegido. Por esto, los matemáticos se dieron cuenta que además del largo del segmento, nos tiene que interesar la inclinación. Lo sé, ya estás estás perdido, ¿inclinación con respecto a qué?
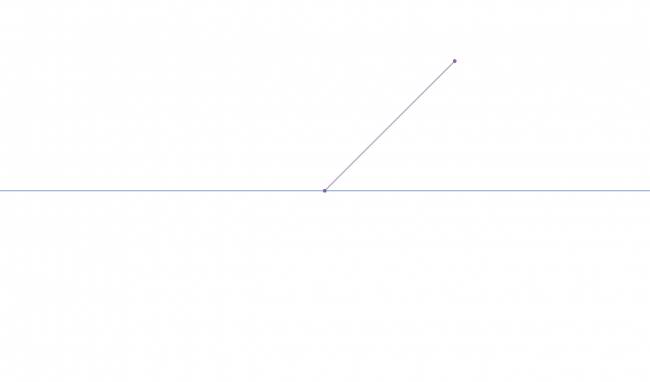
Bueno, vamos a suponer una recta horizontal que pasa por el origen:
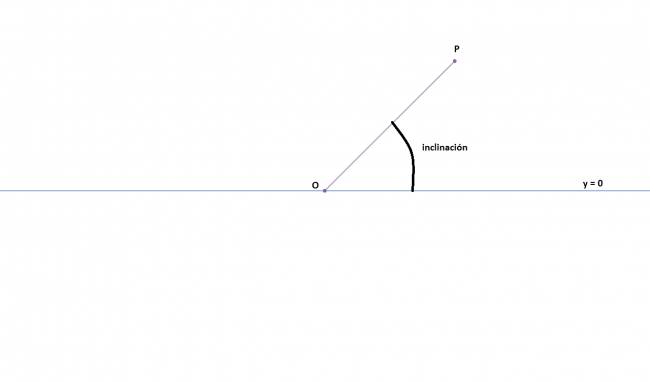
Diremos que la inclinación es el ángulo formado por el segmento entre el origen y el punto, y la recta horizontal.
Bueno, ahora podemos decir que el punto \( P \) es aquel que se encuentra a una determina distancia del origen con una inclinación determinada.
Vamos a aceptar unas convenciones:
· A la distancia de separación del origen al punto la llamaremos con el nombre de módulo y se suele representar con la letra \( r \).
· A la inclinación se la suele representar con la letra griega \( θ \) (pronúnciese títa).
De igual forma que cuando trabajábamos con coordenadas cartesianas teníamos una forma de expresarlas, también la hay para las coordenadas polares: \( P = (r ∠ \theta) \)
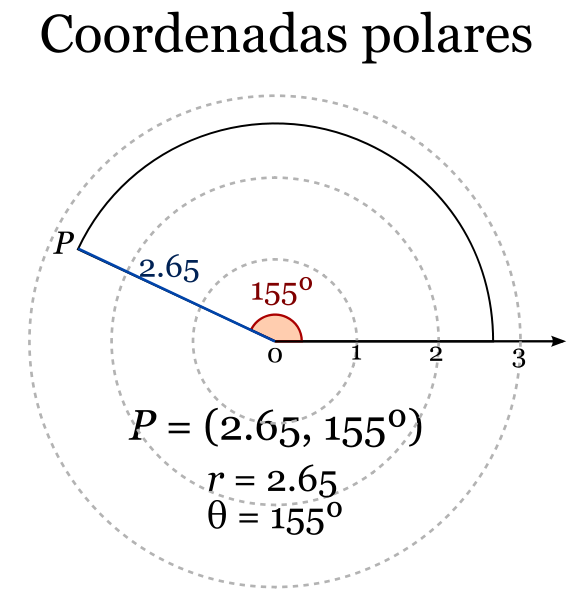
Para conocer este sistema debemos haber trabajado el sistema de ejes cartesianos (el formado por dos rectas perpendiculares).
Repaso del sistema de ejes cartesianos:
Si recordamos, cuando trabajamos con este sistema decíamos: "puedo representar cualquier punto del plano dándole un valor en horizontal y otro en vertical".
Como vemos, grafiqué un punto que tiene coordenadas: 2 en horizontal y 1 en vertical. La notación que usábamos era la siguiente: \( P (2,1) \)
Como siempre digo: \( P \) es para dar un nombre, y generalmente uso tal letra ya que es la inicial de punto.
Ahora sí volvemos a lo que queríamos: coordenadas polares
Las coordenadas polares dicen algo como esto: "puedo representar cualquier punto del plano dándole una distancia de separación con respecto al origen, y la inclinación que este posee". ¡No colapses que ahora explico!
Imaginá un punto fijo, le vas a llamar origen de coordenadas, lo voy a representar con rojo, y ahora quiero que imagine un punto que no sea el anterior, lo voy a representar con anaranjado.
Acá una imagen para que no te pierdas imaginando:
Ahora vamos a trazar un segmento que una ambos puntos:
Ahora me pregunto, la distancia de separación entre el origen y el punto que elegí, ¿es única? No dudes, ¡decí que no!
Suponé estos casos:
Ahí dibujé tres casos, pero podría haber dibujado infinitos segmentos que cumplían la condición de que tenían la misma distancia de separación con en el origen, la cosa es que ese segmento solo no me está diciendo mucho del punto que hace un rato había elegido. Por esto, los matemáticos se dieron cuenta que además del largo del segmento, nos tiene que interesar la inclinación. Lo sé, ya estás estás perdido, ¿inclinación con respecto a qué?
Bueno, vamos a suponer una recta horizontal que pasa por el origen:
Diremos que la inclinación es el ángulo formado por el segmento entre el origen y el punto, y la recta horizontal.
Bueno, ahora podemos decir que el punto \( P \) es aquel que se encuentra a una determina distancia del origen con una inclinación determinada.
Vamos a aceptar unas convenciones:
· A la distancia de separación del origen al punto la llamaremos con el nombre de módulo y se suele representar con la letra \( r \).
· A la inclinación se la suele representar con la letra griega \( θ \) (pronúnciese títa).
De igual forma que cuando trabajábamos con coordenadas cartesianas teníamos una forma de expresarlas, también la hay para las coordenadas polares: \( P = (r ∠ \theta) \)