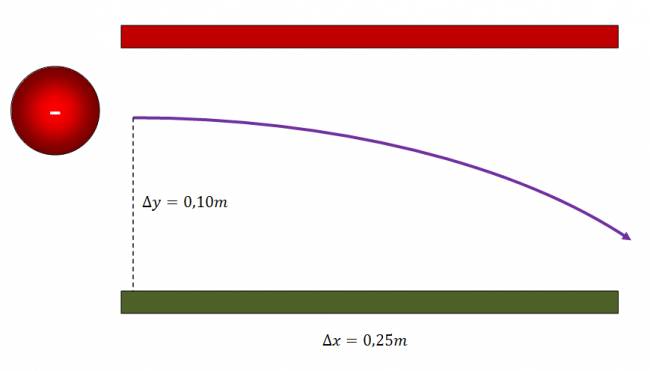
Un electrón que se mueve con una velocidad horizontal de \( v_{ox} = 4,0·10^{6} \frac {m}{s} \), entra en una zona donde existe un campo eléctrico uniforme, creado por dos placas paralelas que lo desvía desde su trayectoria tal como se indica en el dibujo:
a. Determine las características del campo eléctrico creado por las placas.
b. ¿Con qué velocidad abandona el campo eléctrico?
|
Como vemos que se nos está hablando de un electrón ( e- ), recordemos sus características:
\( q_{e^{-}} = -1,6·10^{-19} C \)
\( m_{e^{-}} = 9,1·10^{-31} kg \)
Calculemos el tiempo:
Si recordamos de movimiento de proyectiles, la velocidad en horizontal es constate (MRU), independientemente del movimiento en vertical (principio de independencia de los movimientos de Galileo). Y como ya conocemos la velocidad horizontal, procederé a calcular el desplazamiento horizontal:
$$ v_{x} = \frac {\Delta x}{\Delta t} ⇒ \Delta t = \frac {\Delta x}{v_{x}} ⇒ \Delta t = \frac {0,25 m}{4,0·10^{6} \frac {m}{s}} ⇒ \Delta t = 6,3·10^{-8} s $$
Calculemos la aceleración:
$$ \Delta y = v_{oy}·\Delta t + \frac {a·\Delta t^2}{2} $$
Como la velocidad es horizontal, entonces, la vertical es necesariamente nula:
$$ \Delta y = \frac {a·\Delta t^2}{2} $$
Despejamos para obtener la aceleración:
$$ a = \frac {2·\Delta y}{\Delta t^2} ⇒ a = \frac {2·0,10 m}{6,3·10^{-8} s} ⇒ a = 3,2·10^{-10} \frac {m}{s^2} $$
Si recordamos todavía más, llegaremos a recordar la segunda ley de Newton:
$$ F = m·a $$
Que para nuestro caso sería:
$$ Fe = m_{e^{-}}·a ⇒ Fe = (9,1·10^{-31} kg)·(3,2·10^{-10} \frac {m}{s^2}) ⇒ Fe = 2,9·10^{-40} N $$
Pero a nosotros lo que nos interesa es el campo eléctrico:
$$ E = \frac {Fe}{q} ⇒ E = \frac {2,9·10^{-40} N}{1,6·10^{-19} C} ⇒ E = 1,8·10^{-21} \frac {N}{C} $$
Y el vector es hacia arriba, porque las líneas de campo van desde el plano cargado positivamente al cargado negativamente.
Pero a todo esto, nosotros queremos calcular la velocidad, para esto únicamente debemos hallar la velocidad vertical con la que impacta, porque sabemos que la velocidad horizontal, será la misma al principio que al final.
$$ v_{y} = a·t ⇒ v_{y} = (3,2·10^{-10} \frac {m}{s^2})·(6,3·10^{-8} s) ⇒ v_{y} = 2,0·10^{-17} \frac {m}{s} $$
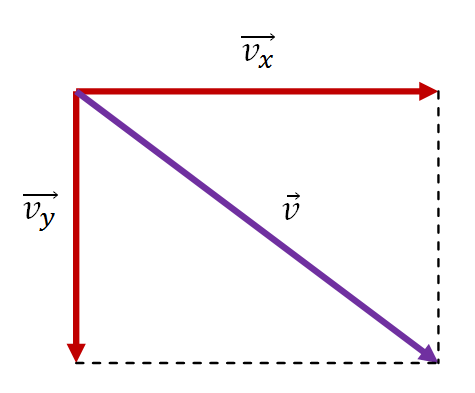
Pero a nosotros nos piden el vector: \( \vec v \) y nosotros sólo tenemos la velocidad en cada uno de los ejes, vamos a calcular la velocidad resultante a partir de estos:
Aplicamos Pitágoras:
$$ v = \sqrt {x_{x}^2 + v_{y}^2} ⇒ v = 4,0·10^{6} \frac {m}{s} $$
Todavía no podemos ser felices, debemos calcular el ángulo de inclinación del vector con respecto a la horizontal, como está por debajo de esta, el ángulo deberá ser negativo.
$$ \tan \alpha = \frac {v_{y}}{v_{x}} = 5,0·10^{24} ⇒ arctan (5,0·10^{24}) = -2,9·10^{-22} º $$
|