06-04-2013, 0:00 AM
El número \( \sqrt {2} \) fue el primer número irracional descubierto por el hombre. Se descubrió al intentar calcular la hipotenusa de un triángulo rectángulo isósceles cuyos catetos median 1 unidad.
Aplicando el teorema de Pitágoras:
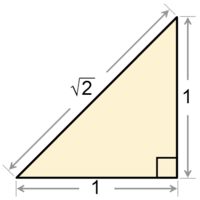
$$ a = \sqrt {b^2 + c^2} ⇒ a = \sqrt {1^2 + 1^2} ⇒ a = \sqrt {2} $$
Esto fue descubierto por uno de los discípulos de Pitágoras de Samos, éste al verse sorprendido, ya que no existía ningún número "perfecto" (se conocía así a los números naturales) que cumpliera esto y ver que contradice la pureza de los números, decidió mandarlo matar.
Pitágoras decía que todo eran números, pero no cualquier número, sino que los números naturales están por todos lados, pero esto no es cierto, por el ejemplo el perímetro de una circunferencia siempre mide un múltiplo de \( \pi \), el cual es el número irracional más conocido.
Recordemos que: un número irracional es todo aquel que no se puede escribir como la división de dos números enteros. Todos los números enteros son números racionales, al número 5 lo puedo escribir de infinitas formas:
$$ 5 = \frac {5}{1} = \frac {10}{2} = \frac {15}{3} = ... $$