28-03-2013, 12:31 PM
La fórmula de Herón de Alejandría permite calcular el área de cualquier triángulo triángulo conociendo los lados de este.
Si recordamos, el área de un triángulo se puede calcular como:
$$ á = \frac {b·h}{2} $$
Así, el área es igual a la mitad del producto de la base por la altura. Si queremos hallar el área de un triángulo rectángulo andamos sobre ruedas, pero si queremos hallar el área de otro tipo de triángulo, primero debemos conocer su altura, para ello hay que calcularla, pero aquí el amigo Herón nos facilita todo esto con su fórmula.
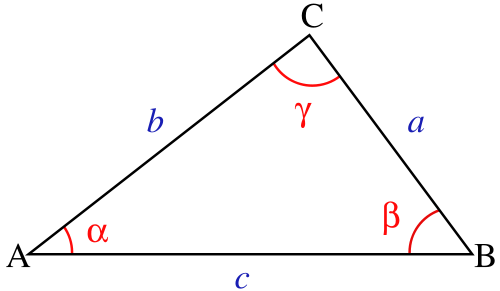
Fórmula de Herón:
$$ á = \sqrt {s·(s-a)·(s-b)·(s-c)} $$
Donde:
$$ s = \frac {a+b+c}{2} $$
También se puede afirmar que \( s \) es la mitad del perímetro total del triángulo.
Si recordamos, el área de un triángulo se puede calcular como:
$$ á = \frac {b·h}{2} $$
Así, el área es igual a la mitad del producto de la base por la altura. Si queremos hallar el área de un triángulo rectángulo andamos sobre ruedas, pero si queremos hallar el área de otro tipo de triángulo, primero debemos conocer su altura, para ello hay que calcularla, pero aquí el amigo Herón nos facilita todo esto con su fórmula.

Fórmula de Herón:
$$ á = \sqrt {s·(s-a)·(s-b)·(s-c)} $$
Donde:
$$ s = \frac {a+b+c}{2} $$
También se puede afirmar que \( s \) es la mitad del perímetro total del triángulo.