| Foro Problemas resueltos Problema de energía (epg, ec, epe) |
| Problema de energía (epg, ec, epe) |
20-09-2012, 6:21 AM
 Un cuerpo de 1,5 kg se desliza por un riel sin rozamiento desde un altura de 5,0 m. El tramo final del riel es horizontal y allí se ha colocado un resorte, de constante elástica, k = 600 N/m, que detiene al cuerpo. a. ¿Cuál es la velocidad del cuerpo antes de tocar al resorte? b. ¿Cuál es la compresión máxima del resorte? |
20-09-2012, 6:45 AM
Este tipo de ejercicio se puede resolver de dos maneras: aplicando el principio de conservación de la energía mecánica o por medio del estudio de la energía en cada tramo del ciclo.
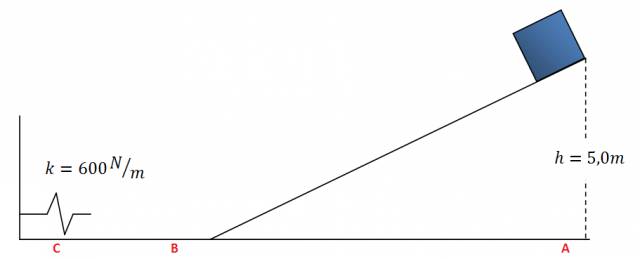
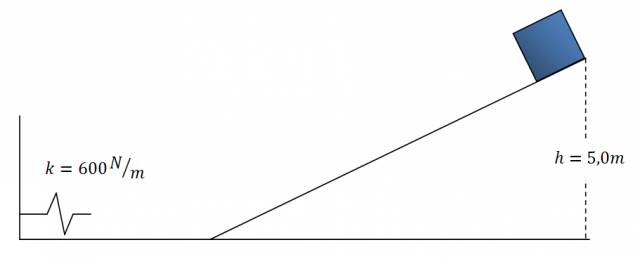
MÉTODO I Estudiaré la energía en cada tramo del trayecto para averiguar lo que me piden. Para facilitar esta tarea nombraré con letras cada tramo:  Mirando la imagen puedo decir que: · EMECA = EpgA · EMECB = EcB · EMECC = EpeC Calcularé EMECA: EMECA = EpgA EpgA = m·g·h EpgA = (1,5 kg)·(10 m/s2)·(5,0 m) EpgA = 75 J La energía que tenía a 5,0 m de altura la convirtió en energía cinética, la cual es igual a la energía potencial gravitatoria porque no hay rozamiento ni ninguna otra fuerza. EMECA = EMECB EMECB = EcB = 75 J EcB = 75 J = 1/2·m·v2 75 J = 1/2·m·v2 75 J = 1/2·(1,5 kg)·v2 (1,5 kg)·v2 = 2·(75 J) (1,5 kg)·v2 = 150 J v2 = (150 J)/(1,5 kg) v2 = 100 m2/s2 v = 10 m/s La energía cinética que tenía la utilizó en para comprimir el resorte, que se convirtió en energía potencial elástica. No actuó ninguna fuerza además del peso, por lo tanto la energía es la misma. EMECB = EMECC EMECC = EpeC = 75 J EpeC = 75 J = 1/2·k·Δlmáx2 75 J = 1/2·k·Δlmáx2 75 J = 1/2·(600 N/m)·Δlmáx2 2·(75 J) = (600 N/m)·Δlmáx2 150 J = (600 N/m)·Δlmáx2 Δlmáx2 = (150 J)/(600 N/m) Δlmáx2 = 0,25 m[/sub]2 Δlmáx = √(0,25 m2) Δlmáx = 0,5 m Quote Respuestas: a. La velocidad del cuerpo antes de tocar al resorte es de 10 m/s. b. La compresión máxima del resorte es 50 cm. |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.