|
   |
| Foro » Departamento de Física » Problemas resueltos » Problema de trabajo: se arrastra una mesa por una mesa con á |
| Problema de trabajo: se arrastra una mesa por una mesa con á |
|
24-02-2013, 5:51 PM
Post: #1
|
|||
|
|||
|
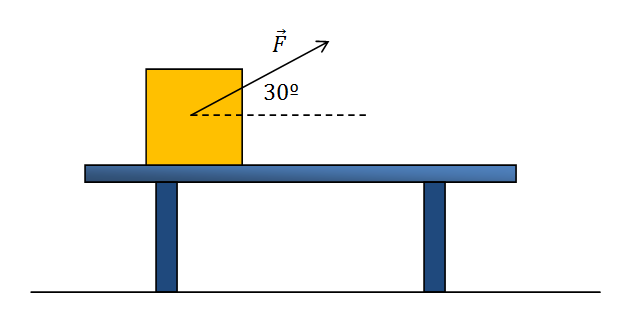
Un joven arrastra una mesa sobre la cual se encuentra apoyada una caja de 25 kg de masa. Ejerce una fuerza de 60 N, mediante una soga que forma un ángulo de 30º con la horizontal. Calcula el trabajo mecánico sobre la caja al desplazarlo 15 m sobre una superficie horizontal, siendo el coeficiente de razonamiento entre el piso y la mesa de 0,2.
|
|||
 |
|
24-02-2013, 5:58 PM
Post: #2
|
|||
|
|||
|
Acá un diagrama para entender de qué se nos está hablando:
 Como siempre, sacamos los datos del problema: \( \Delta \vec x = 15 m \) \( \vec F = 60 N \) \( \alpha = 30º \) \( m = 25 kg \) \( \mu = 0,2 \) Las cosas serían más simples se no hubiera rozamiento, pero lo hay, por lo que vamos a calcularlo: Como estamos hablando de un plano horizontal, podemos afirmar que: $$ \vec N = \vec P = m· \vec g ⇒ \vec N = m· \vec g ⇒ \vec N = (25 kg)·(10 \frac {m}{s^2}) = 250 N ⇒ \vec N = 250 N $$ Recordemos cómo se calcula la fuerza de rozamiento: $$ \vec Froz = \vec N · \mu ⇒ \vec Froz = 250 N · 0,2 = 50 N ⇒ \vec Froz = 50 N $$ 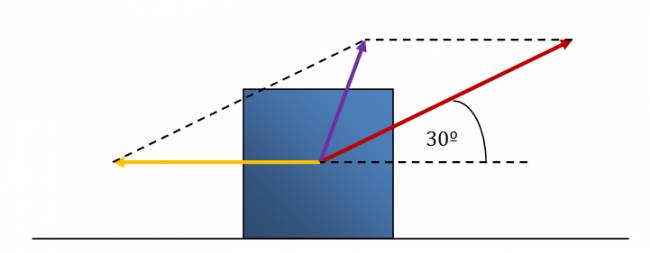Tenemos lo siguiente:  Tenemos que hallar el vector violeta que es la fuerza resultante, para lo cual utilizaremos una variante del teorema del coseno: $$ a = \sqrt {b^2 + c^2 + 2·b·c · \cos \hat A} $$ $$ a = \sqrt {50^2 + 60^2 + 2·50·60 · \cos 150} $$ $$ a = \sqrt {50^2 + 60^2 + 2·50·60 · \cos 150} $$ $$ a = \sqrt {903,84} $$ $$ a = 30 N $$ 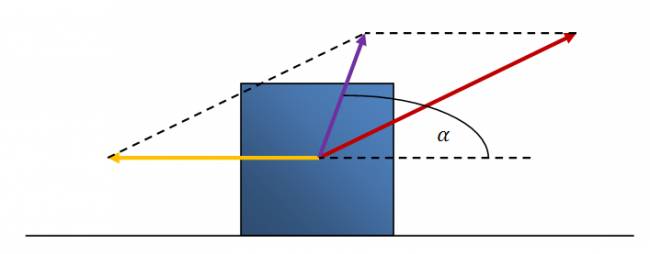Ahora vamos a calcular el ángulo:  El ángulo lo calcularé con el teorema del seno: $$ \frac {a}{sen \hat A} = \frac {b}{sen \hat B} $$ $$ \frac {30}{sen 30º} = \frac {50}{sen \hat B} ⇒ sen \hat B = \frac {50·sen 30º}{30} = 0,84 ⇒ arcsen (0,84) = 57,14º $$ Pero debemos sumar los 30º al ángulo: 57,14º + 30º = 87,14 º. Finalmente, aplicando el teorema del trabajo tenemos que: $$ W_{\vec F} = \vec F · \Delta \vec x · \cos \alpha $$ $$ W_{\vec F} = (30 N) · (15 m) · \cos (87,14º) $$ $$ W_{\vec F} = (30 N) · (15 m) · \cos (87,14º) $$ $$ W_{\vec F} = 23 J $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
 |
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |