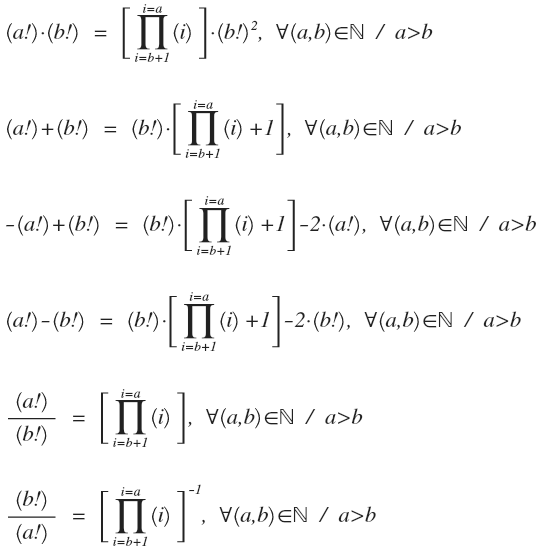16-01-2013, 8:41 PM
Número factorial
Definición:
El factorial de un número \( n \), denotado como \( n! \), es el producto de todos los números naturales desde 1 hasta \( n \).
· Por medio de factores:
$$ n! = n·(n-1)·(n-2)·(n-3)·...·3·2·1 $$
· Utilizando productoria:
$$ n! = \displaystyle\prod_{i=1}^n (i)$$
Demostración de que \( (n-1)! = \frac{n!}{n} \):
Algunas igualdades:
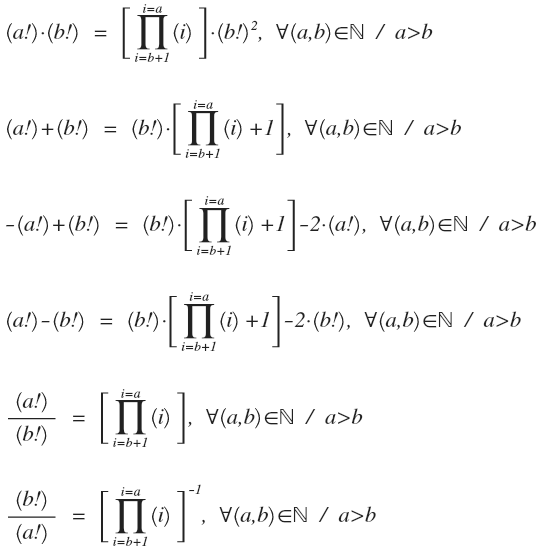
Definición:
El factorial de un número \( n \), denotado como \( n! \), es el producto de todos los números naturales desde 1 hasta \( n \).
· Por medio de factores:
$$ n! = n·(n-1)·(n-2)·(n-3)·...·3·2·1 $$
· Utilizando productoria:
$$ n! = \displaystyle\prod_{i=1}^n (i)$$
Demostración de que \( (n-1)! = \frac{n!}{n} \):
Algunas igualdades: